
在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.

(2)如果AB≠AC,如图,且点D在线段BC上运动.(1)中结论是否成立,为什么?

(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
(1)CF与BD位置关系是垂直;
证明如下:![]() AB=AC,∠ACB=45°,∴∠ABC=45°.
AB=AC,∠ACB=45°,∴∠ABC=45°.
由正方形ADEF得AD=AF,∵∠DAF=∠BAC=90°,
∴∠DAB=∠FAC,∴△DAB≌△FAC,∴∠ACF=∠ABD.
∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(2)CF⊥BD.(1)中结论成立.
理由是:过点A作AG⊥AC交BC于点G,∴AC=AG
可证:△GAD≌△CAF ∴∠ACF=∠AGD=45°
∠BCF=∠ACB+∠ACF=90°.即CF⊥BD

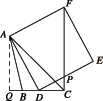
(3)过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,
∵∠BCA=45°,可求出AQ=CQ=4.∴DQ=4-x,
易证△AQD∽△DCP,∴![]() ,∴
,∴![]() ,
,
![]() .
.
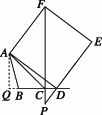
②点D在线段BC延长线上运动时,
∵∠BCA=45°,可求出AQ=CQ=4,∴DQ=4+x.
过A作![]() 交CB延长线于点G,则
交CB延长线于点G,则![]() .
.![]() CF⊥BD,
CF⊥BD,
![]() △AQD∽△DCP,∴
△AQD∽△DCP,∴![]() ,∴
,∴![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=| 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com