
【题目】平面上有3个点的坐标:A(0,﹣3),B(3,0),C(﹣1,﹣4).
(1)在A,B,C三个点中任取一个点,这个点既在直线y1=x﹣3上又在抛物线上y2=x2﹣2x﹣3上的概率是多少?
(2)从A,B,C三个点中任取两个点,求两点都落在抛物线y2=x2﹣2x﹣3上的概率.
【答案】
(1)解:当x=0时,y1=x﹣3=﹣3,y2=x2﹣2x﹣3=﹣3,则A点在直线和抛物线上;
当x=3时,y1=x﹣3=0,y2=x2﹣2x﹣3=0,则B点在直线和抛物线上;
当x=﹣1时,y1=x﹣3=﹣4,y2=x2﹣2x﹣3=0,则C点在直线上,不在抛物线上,
所以在A,B,C三个点中任取一个点,这个点既在直线y1=x﹣3上又在抛物线上y2=x2﹣2x﹣3上的概率= ![]() ;
;
(2)解:画树状图为:

共有6种等可能的结果数,其中两点都落在抛物线y2=x2﹣2x﹣3上的结果数为2,
所以两点都落在抛物线y2=x2﹣2x﹣3上的概率= ![]() =
= ![]() .
.
【解析】(1)先根据一次函数图象上点的坐标特征和二次函数图象上点的坐标特征可判断A、B、C都在直线上,A、B两点在抛物线上,C点不在抛物线上,然后根据概率公式求解;(2)先画树状图展示所有6种等可能的结果数,再找出两点都落在抛物线y2=x2﹣2x﹣3上的结果数,然后根据概率公式求解.
【考点精析】根据题目的已知条件,利用列表法与树状图法和概率公式的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某公司营销A、B两种产品,根据市场调研,发现如下信息: 信息1:销售A种产品所获利润y(万元)与销售产品x(吨)之间存在二次函数关系y=ax2+bx.在x=1时,y=1.4;当x=3时,y=3.6.
信息2:销售B种产品所获利润y(万元)与销售产品x(吨)之间存在正比例函数关系y=0.3x.
根据以上信息,解答下列问题;
(1)求二次函数解析式;
(2)该公司准备购进A、B两种产品共10吨,请设计一个营销方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC= ![]() ,以AB为直径的⊙O分别交BC、AC于点D、E.
,以AB为直径的⊙O分别交BC、AC于点D、E.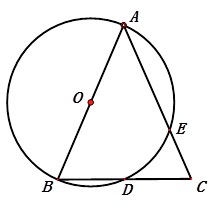
(1)求AE;
(2)过D作DF⊥AC于F,请画出图形,说明DF是否是⊙O的切线,并写出理由;
(3)延长FD,交AB的延长线于G,请画出图形,并求BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A,C重合),DE与AB相交于点F,则图中有( )对相似三角形. 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH= ![]() ,CH=5
,CH=5 ![]() .
. 
(1)求证:AH是⊙O的切线;
(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;
(3)在(2)的条件下,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF. 
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E. 
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com