
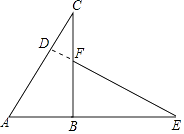
【题目】如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答: 
(1)旋转中心是点 , 旋转的最小角度是度
(2)AC与EF的位置关系如何,并说明理由.
【答案】
(1)B;90
(2)解:AC⊥EF 理由如下:
延长EF交AC于点D由旋转可知∠C=∠E
∵∠ABC=90°
∴∠C+∠A=90°
∴∠E+∠A=90°
∴∠ADE=90°
∴AC⊥EF.
【解析】解:(1)∵BC=BE,BA=BF,
∴BC和BE,BA和BF为对应边,
∵△ABC旋转后能与△FBE重合,
∴旋转中心为点B;
∵∠ABC=90°,
而△ABC旋转后能与△FBE重合,
∴∠ABF等于旋转角,
∴旋转了90度,
所以答案是:B,90;
【考点精析】认真审题,首先需要了解旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了).


科目:初中数学 来源: 题型:
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |
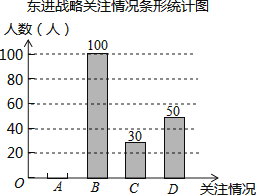
(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC. 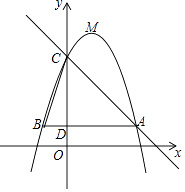
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
(1)当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,直接写出结论:AE DB
(填“>”,“<”或“=”).
(2)证明你得出的以上(1),如图2,过点E作EF∥BC,交AC于点F.

(3)在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED = EC.若△ABC的边长为1,AE = 2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.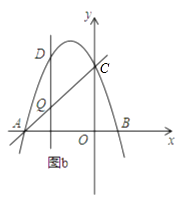
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com