
���� ��1�����ݡ��Ͷ������Ķ��弰��λ�����ص㼴�ɵó����ۣ�
��2���������λ����Ȼ���жϳ�����λ������7�������������ɣ�
��� �⣺��1���ߡ��Ͷ���������λ��������λ��Ҫ��С����λ��С��1��ʮλ��С��0��
�������С�ġ��Ͷ�����Ϊa��
�ɡ��Ͷ������Ķ���ã�1��2+3��0+a=2+a��
��2+a�ܱ�7��������Ҫ��С��
��2+a=7��
��a=5��
����С�ġ��Ͷ�����Ϊ 105��
�ʴ�Ϊ��105��
��2��4+3��4+8=28����28�ܱ�7������
��448�ǡ��Ͷ�������
��2����һ�����Ͷ�����Ϊ$\overline{abc}$��
��2a+3b+c�ܱ�7������
��2a+3b+c��7�ı�����
��$\frac{100a+10b+c}{7}$=$\frac{98a+2a+7b+3b+c}{7}$=$\frac{��98a+7b��+��2a+3b+c��}{\;}$=14a+b+$\frac{2a+3b+c}{7}$��
��a��b��$\frac{2a+3b+c}{7}$��������
�ࡰ�Ͷ�����Ϊ$\overline{abc}$�ܱ�7������
���� ������Ҫ��������λ���ı�ʾ���������⣬�¶��壬�Ȿ��Ĺؼ��������Ӧ���¶��塰�Ͷ�������


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
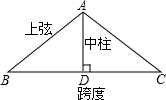 ��ͼ�������ݶ����ּܣ����������Σ��Ŀ��Ϊ20m����B=37�㣬������AD��DΪ�ױ��е㣩������AB�ij����ο����ݣ�cos37���0.6��
��ͼ�������ݶ����ּܣ����������Σ��Ŀ��Ϊ20m����B=37�㣬������AD��DΪ�ױ��е㣩������AB�ij����ο����ݣ�cos37���0.6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 80 | 75 | 90 | 64 | 88 | 95 |
| �� | 84 | 80 | 88 | 76 | 79 | 85 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
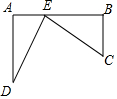 ��ͼ����·��A��B��վ����Ϊ�������㣩���25ǧ�ף�C��DΪ��·ͬ��������ׯ����Ϊ���㣩��DA��AB��A�㣬CB��AB��B�㣬DA=15ǧ�ף�CB=10ǧ�ף�����Ҫ����·AB����һ������Ʒ�ع�վE��ʹC��D����ׯ��Eվ�ľ�����ȣ���EվӦ���ھ�Aվ10ǧ�״���
��ͼ����·��A��B��վ����Ϊ�������㣩���25ǧ�ף�C��DΪ��·ͬ��������ׯ����Ϊ���㣩��DA��AB��A�㣬CB��AB��B�㣬DA=15ǧ�ף�CB=10ǧ�ף�����Ҫ����·AB����һ������Ʒ�ع�վE��ʹC��D����ׯ��Eվ�ľ�����ȣ���EվӦ���ھ�Aվ10ǧ�״����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
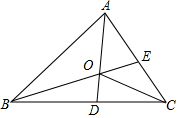 ��ͼ��AD��BE�ǡ�ABC�Ľ�ƽ�����ҽ��ڵ�O������OC�����������۶ϣ�
��ͼ��AD��BE�ǡ�ABC�Ľ�ƽ�����ҽ��ڵ�O������OC�����������۶ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
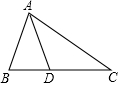 ��֪����ͼ���ڡ�ABC�У�AD�����Ľ�ƽ���ߣ�AB=6cm��AC=8cm���� S��ABD��S��ACD=��������
��֪����ͼ���ڡ�ABC�У�AD�����Ľ�ƽ���ߣ�AB=6cm��AC=8cm���� S��ABD��S��ACD=��������| A�� | 4��3 | B�� | 3��4 | C�� | 16��9 | D�� | 9��16 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com