
分析 先将原式化简,然后求出该分式有意义时,a的取值范围即可求出答案.
解答 解:原式=(1+$\frac{1}{a-1}$)÷$\frac{a}{(a-1)^{2}}$
=(1+$\frac{1}{a-1}$)×$\frac{(a-1)^{2}}{a}$
=$\frac{(a-1)^{2}}{a}$+$\frac{a-1}{a}$
=$\frac{{a}^{2}-2a+1+a-1}{a}$
=$\frac{{a}^{2}-a}{a}$
=a-1
∵$\left\{\begin{array}{l}{a-1≠0}\\{a≠0}\end{array}\right.$,
∴a≠0且a≠1,
∵0≤a<4
∴a=2时,
原式=1
点评 本题考查分式的化简运算,解题的关键是将原式分式化简,本题属于基础题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
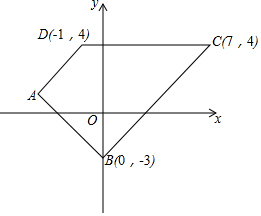 图中的A(-4,1)、B(0,-3)、C(7,4)和D(-1,4)是一个梯形的顶点.其中AD∥BC及AB⊥AD.
图中的A(-4,1)、B(0,-3)、C(7,4)和D(-1,4)是一个梯形的顶点.其中AD∥BC及AB⊥AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
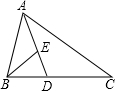 如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )
如图,△ABC中,D、E两点分别在BC、AD上,且AD平分∠BAC,若∠ABE=∠C,AD:ED=3:1,则△BDE与△ADC的面积比为( )| A. | 16:45 | B. | 2:9 | C. | 1:9 | D. | 1:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com