
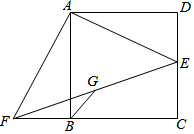
 E为正方形ABCD的边CD上的一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:
E为正方形ABCD的边CD上的一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:分析 如图,取AF的中点P,连接PG,CG,在线段BC上取一点N,使得BF=BN,连接EN、BD.
①正确.只要证明PG=$\frac{1}{2}$AF即可.
②正确.只要证明EN=$\sqrt{2}$EC,EN=2BG即可.
③正确.只要证明EN∥BD,EN∥BG即可.
④正确.设BC=CD=a,DE=b,由S四边形BGEC=$\frac{1}{4}$S四边形ABCD,得S△BGC+S△ECG=$\frac{1}{4}$a2,即$\frac{1}{2}$•a•$\frac{1}{2}$•(a-b)+$\frac{1}{2}$•$\frac{1}{2}$(a+b)•(a-b)=$\frac{1}{4}$a2,即b2+ab-a2=0,
解得b=$\frac{\sqrt{5}-1}{2}$a或b=$\frac{-\sqrt{5}-1}{2}$a(舍弃),由此即可解决问题.
解答 解:如图,取AF的中点P,连接PG,CG,在线段BC上取一点N,使得BF=BN,连接EN、BD.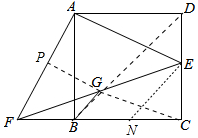
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠ABF=∠DCB=90°,
∵AP=PF,
∴点P是△ABF的外心,
∵AP=PF,FG=GE,
∴PG=$\frac{1}{2}$AE=$\frac{1}{2}$AF,
∴点G在△ABF的外接圆上,故①正确,
∵BF=BN=DE,BC=CD,
∴CN=CE,EN=$\sqrt{2}$EC,
∵FG=GE,FB=BN,
∴EN=2BG,
∴2BG=$\sqrt{2}$EC,
∴EC=$\sqrt{2}$BG,故②正确,
∵CN=CE,∠BCD=90°,
∴∠ENC=∠DBC=45°,
∴NE∥BD,又∵EN∥BG,
∴B、G、D共线,故③正确,
设BC=CD=a,DE=b,
∵S四边形BGEC=$\frac{1}{4}$S四边形ABCD,
∴S△BGC+S△ECG=$\frac{1}{4}$a2,
∴$\frac{1}{2}$•a•$\frac{1}{2}$•(a-b)+$\frac{1}{2}$•$\frac{1}{2}$(a+b)•(a-b)=$\frac{1}{4}$a2,
∴b2+ab-a2=0,
解得b=$\frac{\sqrt{5}-1}{2}$a或b=$\frac{-\sqrt{5}-1}{2}$a(舍弃),
∴DE=$\frac{\sqrt{5}-1}{2}$CD,
∴点E是CD的黄金分割点,故④正确.
故答案为①②③④.
点评 本题考查圆综合题、旋转变换、正方形的性质、等腰直角三角形的性质、三角形的中位线定理、三角形的外接圆等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,锐角△ABC是⊙O内接三角形,弦AE⊥BC,垂足为D.在AD上取点F,使FD=DE,连接CF,并延长交AB于点G.求证:CG⊥AB.
如图,锐角△ABC是⊙O内接三角形,弦AE⊥BC,垂足为D.在AD上取点F,使FD=DE,连接CF,并延长交AB于点G.求证:CG⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种 食物 | 乙种 食物 | 丙种 食物 | 每千克生产成本(元) | |||
| 甲种食物 | 9 | |||||
| 维生素A(单位/千克) | 400 | 600 | 400 | 乙种食物 | 12 | |
| 维生素B(单位/千克) | 800 | 200 | 400 | 丙种食物 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com