
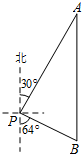 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05) 分析 首先过点P作PC⊥AB于点C,然后利用三角函数的性质:PC=AP•sin30°,即可求得PC的值,再由PB=$\frac{PC}{sin64°}$,即可求得答案.
解答 解: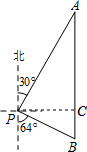 过点P作PC⊥AB于点C.
过点P作PC⊥AB于点C.
由题意可知,AB∥PD,
∴∠A=30°,∠B=64°,
在Rt△APC中,∠ACP=90°,∠A=30°,AP=80,
∴PC=AP•sin30°=80×$\frac{1}{2}$=40,
在Rt△PBC中,∠BCP=90°,∠B=64°,
∴PB=$\frac{PC}{sin64°}$=$\frac{40}{0.9}$=44.44≈44.4(海里).
答:海轮所在的B处与灯塔P的距离约为44.4海里.
点评 此题考查了方向角问题.注意准确构造直角三角形是解此题的关键.


科目:初中数学 来源: 题型:填空题
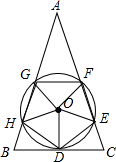 如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.
如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
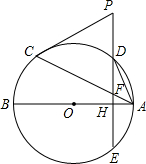 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
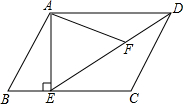 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
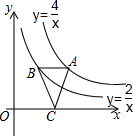 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com