
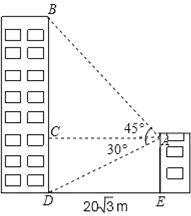
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20![]() 米.
米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
【答案】(1)大厦的高度BD为:(20![]() +20)米;
+20)米;
(2)小敏家的高度AE为20米.
【解析】试题分析:(1)易得四边形AEDC是矩形,即可求得AC的长,然后分别在Rt△ABC与Rt△ACD中,利用三角函数的知识求得BC与CD的长,继而求得答案;
(2)结合(1),由四边形AEDC是矩形,即可求得小敏家的高度AE.
试题解析:(1)如图,∵AC⊥BD,
∴BD⊥DE,AE⊥DE,
∴四边形AEDC是矩形,
∴AC=DE=20![]() 米,
米,
∵在Rt△ABC中,∠BAC=45°,
∴BC=AC=20![]() 米,
米,
在Rt△ACD中,tan30°=![]() ,
,
∴CD=ACtan30°=20![]() ×
×![]() =20(米),
=20(米),
∴BD=BC+CD=20![]() +20(米);
+20(米);
∴大厦的高度BD为:(20![]() +20)米;
+20)米;
(2)∵四边形AEDC是矩形,
∴AE=CD=20米.
∴小敏家的高度AE为20米.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
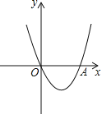
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4. (1)求该抛物线的解析式; (2)若线段OA绕点O顺时针旋转45°到OA′,试判断点A′是否在该抛物线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a,如min{1,﹣4}=﹣4,min{﹣6,﹣2}=﹣6,则min{﹣x2+2,﹣2x}的最大值为( )
A. 2![]() ﹣2 B.
﹣2 B. ![]() +1 C. 1﹣
+1 C. 1﹣![]() D. 2
D. 2![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
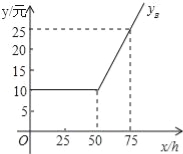
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为正
为正![]() 的
的![]() 边上一点(
边上一点(![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别在边
分别在边![]() 上,且
上,且![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() (用含
(用含![]() 的式子表示);
的式子表示);
(3)如图2,若点![]() 为
为![]() 边的中点,求证:
边的中点,求证: ![]() .
.
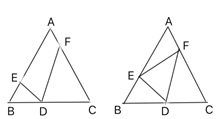
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com