
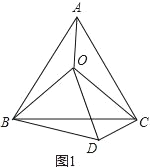
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
【答案】(1)①60°;②4;③150°;(2)OA2+2OB2=OC2时,∠ODC=90°,理由详见解析.
【解析】
(1)①△ABO旋转后AB与BC重合,根据旋转的性质可知∠ABC是旋转角,由△ABC是等边三角形即可知答案.②由旋转的性质可知OB=BD,根据旋转角是60°可知∠OBD=60°即可证明△BOD是等边三角形,进而求出OD的长.③根据OD=4,OC=5,CD=3可证明△OCD是直角三角形,根据△BOD是等边三角形即可求出∠BDC得度数.(2)根据旋转的性质可知旋转角为90°,可证明三角形BOD是等腰直角三角形,进而求出OD=![]() OB,根据△OCD是直角三角形即可知答案.
OB,根据△OCD是直角三角形即可知答案.
(1)①∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=60°,
∴旋转角的度数为60°;
②∵△BAO绕点B顺时针旋转后得到△BCD,
∴BO=BD,
而∠OBD=60°,
∴△OBD为等边三角形;
∴OD=OB=4;
③∵△BOD为等边三角形,
∴∠BDO=60°,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴CD=AO=3,
在△OCD中,CD=3,OD=4,OC=5,
∵32+42=52,
∴CD2+OD2=OC2,
∴△OCD为直角三角形,∠ODC=90°,
∴∠BDC=∠BDO+∠ODC=60°+90°=150°;
(2)OA2+2OB2=OC2时,∠ODC=90°.理由如下:
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD,CD=AO,
∴△OBD为等腰直角三角形,
∴OD=![]() OB,
OB,
∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°,
∴OA2+2OB2=OC2,
∴当OA、OB、OC满足OA2+2OB2=OC2时,∠ODC=90°.


科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.

(1)图②中的阴影部分的面积为________;
(2)观察图②,三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是________;
(3)观察图③,你能得到怎样的代数等式呢?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n);
(5)若x+y=﹣6,xy=2.75,求x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() 、
、![]() 、
、![]() 满足
满足![]() .
.
(1)若![]() 没有平方根,判断点
没有平方根,判断点![]() 在第几象限并说明理由;
在第几象限并说明理由;
(2)若点![]() 到
到![]() 轴的距离是点
轴的距离是点![]() 到
到![]() 轴距离的
轴距离的![]() 倍,求点
倍,求点![]() 的坐标;
的坐标;
(3)点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2.8+(﹣3.6)+(+3)﹣(﹣3.6)
(2)(﹣4)2010×(﹣0.25)2009+(﹣12)×(![]() ﹣
﹣![]() +
+![]() )
)
(3)13°16'×5﹣19°12'÷6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com