Question

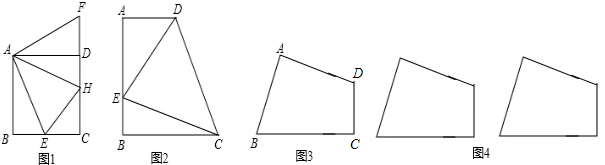
课本练习拓展：
（1）如图1，在正方形ABCD中，E是BC上的一点，△ABE经过旋转后得到△ADF，
①旋转中心是点

A

；旋转角度最少是

90

度．
②爱动脑筋的小兵，在CD边上取点H使得∠HAE=45°，他发现：HE=BE+HD，他的发现正确吗？请你判断并说明理由．
（2）思维闯关：
如图2，在直角梯形ABCD中AD∥BC（BC＞AD），∠B=90°BC=AB=6，E是 AB上一点，且∠DCE=45°，BE=2，则DE的长=

5

．（小兵运用解答（1）中所积累的经验和知识做出了该题）
（3）动手闯过：
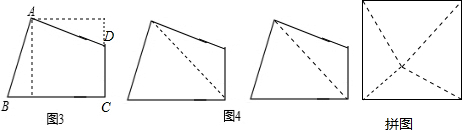
①小明有一块如图3所示的纸片，其中∠A=∠C=90°，AB=AD．小明请小兵只剪一刀后把它拼成正方形，请你帮助小兵在图中画出剪拼得示意图．
②小兵好朋友小红现有两块同小明一样的纸片，如图4，小兵能否在每块上各剪一刀，然后拼成一个大的正方形？若能，请你画出剪法和拼法的示意图；若不能，简要说明理由．

Answer 1

分析：（1）①根据图形可直接得到结论；
②首先证明△FAH≌△EAH，根据全等三角形的性质可得FH=EH，再根据旋转中线段的相等关系进行等量代换即可得到结论；
（2）过C作CG⊥AD，交AD延长线于G，先根据有一组邻边相等的矩形是正方形证四边形ABCG是正方形．再设DE=x，利用（1）中②的结论，在Rt△AED中利用勾股定理可求出DE
（3）①画出示意图，只要求出△ABE≌△ADF，再根据此条件求出四边形AECF是正方形即可；
②根据题意画出示意图即可，此时正方形的面积等于两块涂料面积的和．

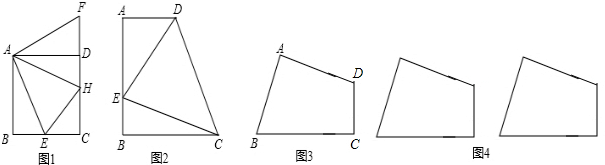
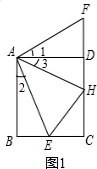解答：解：（1）①旋转中心是点A；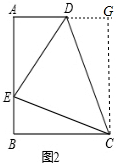
旋转角度最少是90度；

②如图1，
∵∠EAH=45°，∠BAD=90°，
∴∠2+∠3=45°，
∠1=∠2，
∵∠DAB=90°，
∴∠FAE=90°，
∴∠1+∠3=90°-45°=45°，
∴∠FAH=∠EAH，
在△FAH和△EAH中

AF=AE ∠FAH=∠EAH AH=AH

，
∴△FAH≌△EAH（SAS），
∴FH=EH，
即FD+DH=EH，
∵FD=BE，
∴EB+DH=EH；

（2）如图2，过C作CG⊥AD于G，
在直角梯形ABCD中，
∵∠A=∠B=90°，∠CGA=90°，
∴四边形ABCG为矩形，
∵AB=BC，
∴四边形ABCG为正方形，
∴AG=BC=6，
∵∠DCE=45°，由（1）中②的结论可得ED=BE+DG，
设DE=x，则DG=x-2，
∴AD=8-x，
在Rt△AED中，∵DE²=AD²+AE²，
∴x²=（8-x）²+4²
∴x=5，
即DE=5．

（3）①如图3所示：
②如图4所示：
．

点评：此题主要考查了图形的旋转，全等三角形的判定与性质，正方形的判定与性质，勾股定理，以及图形的剪拼，是一道不错的综合题．