练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD等于　　海里．


    10         解：根据题意可知∠CAD=30°，∠CBD=60°，

    ∵∠CBD=∠CAD+∠ACB，

    ∴∠CAD=30°=∠ACB，

    ∴AB=BC=20海里，

    在Rt△CBD中，∠BDC=90°，∠DBC=60°，sin∠DBC=，

    ∴sin60°=，

    ∴CD=12×sin60°=20×=10海里，

    故答案为：10．

    点评：        本题考查了解直角三角形的应用，难度适中．解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，若|cosA﹣|+（1﹣tanB）2=0，则∠C的度数是（　　）

    A．  45°          B．60°          C．75°          D． 105°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，梯子斜靠在与地面垂直（垂足为O）的墙上，当梯子位于AB位置时，它与地面所成的角∠ABO=60°；当梯子底端向右滑动1m（即BD=1m）到达CD位置时，它与地面所成的角∠CDO=51°18′，求梯子的长．

    （参考数据：sin51°18′≈0.780，cos51°18′≈0.625，tan51°18′≈1.248）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，Rt△ABC中，∠ACB=90°，CD是AB上中线，若CD=5，AC=8，则sinA为（　　）

    A．              B．            C．            D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    根据道路管理规定，在羲皇大道秦州至麦积段上行驶的车辆，限速60千米/时．已知测速站点M距羲皇大道l（直线）的距离MN为30米（如图所示）．现有一辆汽车由秦州向麦积方向匀速行驶，测得此车从A点行驶到B点所用时间为6秒，∠AMN=60°，∠BMN=45°．

    （1）计算AB的长度．

    （2）通过计算判断此车是否超速．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（　　）

    A．  16cm          B．18cm          C．20cm          D． 22cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，AB=BC，将△ABC沿直线BC平移到△DCE（使B与C重合），连接BD，求∠BDE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


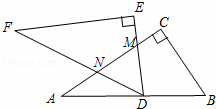
    如图，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，如图，将△DEF绕点D旋转，点D与AB的中点重合，DE，DF分别交AC于点M，N，使DM=MN，则重叠部分（△DMN）的面积为　　．

    查看答案和解析>>

    同步练习册答案