
| A. | 设上坡路长x千米,可列方程$\frac{x}{3}-\frac{x}{5}=\frac{54}{60}-\frac{42}{60}$ | |
| B. | 设上坡路长x千米,平路长y千米,可列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$ | |
| C. | 列算式(54-42)÷(5-3)即可求出上坡路长. | |
| D. | 根据条件,能求出甲地到乙地的全程是3.1千米. |
分析 去乙地时的路程和回来时是相同的,不过去时的上坡路和下坡路和回来时恰好相反,平路不变,已知上下坡的速度和平路速度,根据去时和回来时的时间关系,可列出方程组.
解答 解:设从甲地到乙地上坡与平路分别为xkm,ykm,
由题意得:列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$,
不能通过列算式(54-42)÷(5-3)求出上坡路长,
故选C
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.


科目:初中数学 来源: 题型:选择题
| A. | 一象限 | B. | 二象限 | C. | 三象限 | D. | 四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省成都市金堂县八年级上学期期末考试数学试卷就(解析版) 题型:填空题
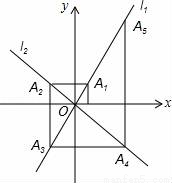
如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线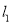 ,
, 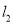 ,过点(1,0)作x轴的垂线交
,过点(1,0)作x轴的垂线交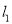 于点A1,过点A1作y轴的垂线交
于点A1,过点A1作y轴的垂线交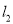 于点A2,过点A2作x轴的垂线交
于点A2,过点A2作x轴的垂线交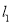 于点A3,过点A3作y轴的垂线交
于点A3,过点A3作y轴的垂线交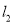 于点A4,…依次进行下去,则点A2015的坐标为__.
于点A4,…依次进行下去,则点A2015的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -$\sqrt{3}$-$\sqrt{2}$ | D. | $\sqrt{2}$-$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com