
【题目】如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是____.

科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1交y轴于点P.
(1)过点P作与x轴平行的直线,交抛物线于点Q,PQ=4,求![]() 的值;
的值;
(2)横纵坐标都是整数的点叫做整点.在(1)的条件下,记抛物线与x轴所围成的封闭区域(不含边界)为W.若区域W内恰有4个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 号楼在
号楼在![]() 号楼的南侧,两楼高度均为
号楼的南侧,两楼高度均为![]() 楼间距为
楼间距为![]() .冬至日正午,太阳光线与水平面所成的角为
.冬至日正午,太阳光线与水平面所成的角为![]() .
.![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() ,春分日正午,太阳光线与水平面所成的角为
,春分日正午,太阳光线与水平面所成的角为![]() ,
,![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() .已知
.已知![]() .
.
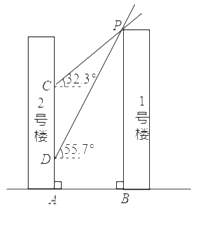
(1)求楼间距![]() ;
;
(2)若![]() 号楼共
号楼共![]() 层,层高均为
层,层高均为![]() 则点
则点![]() 位于第几层? ( 参考数据:
位于第几层? ( 参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作)BD是矩形ABCD的对角线,AB=4,BC=3.将△BAD绕着点B顺时针旋转α度(0°<α<360°)得到△BEF,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则DE=______.
(探究)当点E落在线段DF上时,CD与BE交于点G.其它条件不变,如图②.
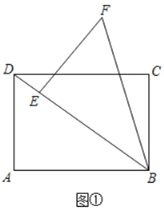
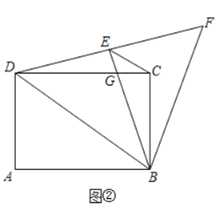
(1)求证:△ADB≌△EDB;
(2)CG的长为______.
(拓展)连结CF,在△BAD的旋转过程中,设△CEF的面积为S,直接写出S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,市场上防护口罩出现热销.某药店用![]() 元购进甲,乙两种不同型号的口罩共
元购进甲,乙两种不同型号的口罩共![]() 个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的
个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的![]() 倍.
倍.
![]() 求购进的甲,乙两种口罩的单价各是多少?
求购进的甲,乙两种口罩的单价各是多少?
![]() 若甲,乙两种口罩的进价不变,该药店计划用不超过
若甲,乙两种口罩的进价不变,该药店计划用不超过![]() 元的资金再次购进甲,乙两种口罩共
元的资金再次购进甲,乙两种口罩共![]() 个,求甲种口罩最多能购进多少个?
个,求甲种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.
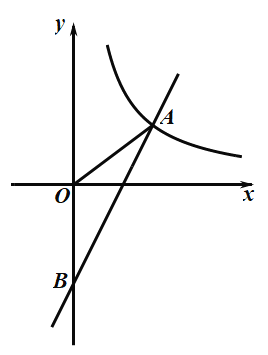
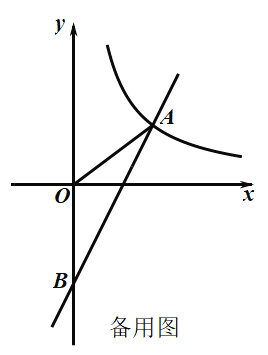
(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com