
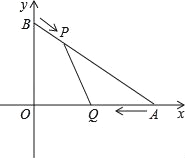
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪��A��4��0������B��0��3������P�ӵ�B������BA�������A�����˶����ٶ�Ϊÿ��1����λ���ȣ���Q�ӵ�A������AO�������O�����˶����ٶ�Ϊÿ��2����λ���ȣ�����PQ�������˶���ʱ��Ϊt�루0��t��2����
��1����ֱ��AB�Ľ���ʽ��
��2�����AQP�����Ϊy����y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ�߶�PQǡ�ðѡ�AOB���ܳ������ͬʱƽ�֣������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
��4������PO�����ѡ�PQO��QO���ۣ��õ��ı���PQP��O����ô�Ƿ����ijһʱ��t��ʹ�ı���PQP��OΪ���Σ������ڣ��������ʱ��Q����������εı߳����������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x+3����2��y����
x+3����2��y����![]() t2+3t����3��������ijһʱ��t��ʹ�߶�PQǡ�ð���AOB���ܳ������ͬʱƽ�֣����ɼ���������4������ijһʱ��t��ʹ�ı���PQP'OΪ���Σ���Q��������(
t2+3t����3��������ijһʱ��t��ʹ�߶�PQǡ�ð���AOB���ܳ������ͬʱƽ�֣����ɼ���������4������ijһʱ��t��ʹ�ı���PQP'OΪ���Σ���Q��������(![]() ),����PQP��O�ı߳�Ϊ
),����PQP��O�ı߳�Ϊ![]() ��
��
��������
��1����֪��A��B��������꣬���ô���ϵ�������ֱ��AB�Ľ���ʽ��
��2��������APQ�У��ױ�AQ�ij���֪���ؼ�����P���������ֵ����P��PM��OA��M��ͨ�����������������εó��ijɱ����߶Σ������PM�ij��������ɸ��������ε������ʽ���y��t�ĺ�����ϵʽ��
��3�����÷�������⣮�ȼ������������tֵ�����ڴ�ʱPQ��������ABO���ܳ�ƽ�֣����BP+BO+OQ=AP+AQ���ݴ˿����t��ֵ��Ȼ��t��ֵ�����루2���ĺ�����ϵʽ�У�����ʱ������APQ������Ƿ����������AOB�������һ�뼴�ɣ�
��4������ı���OPQP�������Σ���ô��Ҫ�����������OP=PQ����ôPM��ֱƽ��OQ����ʱQM=OQ���ɽ���OA�ij�����t��ֵ����P��PN��OB��N����ô������BNP��������BOA���ƣ������PN�ı���ʽ��Ҳ�������QM��MO�ı���ʽ���ɸ���OA=OM+QM+AQ�������ʱt��ֵ��������������εı߳���
��1����ֱ��AB�Ľ���ʽΪy��kx+b��
��![]()
���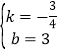 ��
��
��ֱ��AB�Ľ���ʽ��![]() ��
��
��2����Rt��AOB��AB��![]() ��5��
��5��
�����⣬��BP��t��AP��5��t��AQ��2t��
����P��PM��AO��M��
�ߡ�APM�ס�ABO��
��![]() ��
��
��![]() ��
��
��PM��3��![]() t��
t��
��y��![]() AQPM��
AQPM��![]() 2t��3��
2t��3��![]() t������
t������![]() t2+3t��
t2+3t��
��3��������ijһʱ��
��PQ����AOB�ܳ�ƽ�֣���AP+AQ��BP+BO+OQ��
����5��t��+2t��t+3+��4��2t����
���t��1��
��PQ����AOB���ƽ�֣���S��APQ��![]() S��AOB��
S��AOB��
����![]() t2+3t��3��
t2+3t��3��
��t��1�������淽�̲�������
��������ijһʱ��t��ʹ�߶�PQ����AOB���ܳ������ͬʱƽ�֣�
��4������ijһʱ��t��ʹ�ı���PQP'OΪ���Σ�
����P��PN��BO��N��
���ı���PQP��O�����Σ�����PQ��PO��
��PM��AO��M��
��QM��OM��
��PN��BO��N���ɵ���PBN�ס�ABO��
��![]() ��
��
��![]() ��
��
��PN��![]() t��
t��
��QM��OM��![]() t��
t��
��![]() t+
t+![]() t+2t��4��
t+2t��4��
��t��![]() ��
��
����t��![]() ʱ���ı���PQP��O�����Σ�
ʱ���ı���PQP��O�����Σ�
��OQ��4��2t��![]() ��
��
����Q�������ǣ�![]() ��0����
��0����
��PM��3��![]() t��
t��![]() ��OM��
��OM��![]() t��
t��![]() ��
��
��Rt��PMO��PO��![]() ��
��![]() ��
��![]() ��
��
������PQP��O�ı߳�Ϊ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����ﹲ��3��������2������1���������dz���ɫ�����ͬ��
��1������������������һ�����ǰ���ĸ����Ƕ��٣�
��2������������������һ���������Ż����ӣ����Ⱥ�������һ����������������Ķ��ǰ���ĸ��ʣ���������״ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
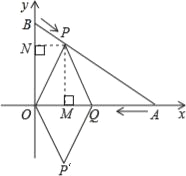
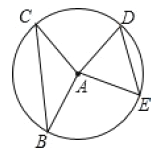
����Ŀ����ѧ����ѧϰ��Բ�ܽǵĸ�������ʣ���������Բ�ϣ�������Բ�ཻ������ͬ�����Ե�Բ�ܽ��������С���ڿκ������Բ��Ǻ�Բ�ڽǽ�����̽����
����������̽�����̣��벹��������
������������Բ�⣬������Բ�ཻ�Ľǽ���Բ��ǣ�������Բ�ڣ�������Բ�ཻ�Ľǽ���Բ�ڽǣ���ͼ1����MΪ![]() ���Ե�һ��Բ��ǣ�
���Ե�һ��Բ��ǣ�
(1)����ͼ2�л���![]() ���Ե�һ��Բ�ڽǣ�
���Ե�һ��Բ�ڽǣ�
�������
(2)ͨ����λ�ͼ��������������������룺һ�������Ե�Բ���______���������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽ�______���������Ե�Բ�ܽǣ�(������������������������С����)
����֤����
(3)����ͼ1��ͼ2��������������������ѡһ������֤����
������
����֤���������������붼����ȷ�ģ�����̽�����֣������Խ����������⣮
(4)��ͼ3��F��H�ǡ�CDE�ı�DC�����㣬�ڱ�DE����һ��Pʹ�á�FPH�����������ȷ����P��λ�ã�(д��˼·���ɣ���Ҫ��д�������ͻ�ͼ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ͬ���˿��ƣ�ÿ�����ţ������Ƶ��������ֱַ���2��3����ÿ�����и��������һ���ƣ���Ϊһ�����飮
��1��С����С����һ����������Ϸ���������������������ͬС���ʤ������С����ʤ�������б�������״ͼ�ķ���˵�������Ϸ�Ƿ�ƽ��
��2��С����Ϊ������һ�������У������Ƶ��������ֺͿ���Ϊ4��5��6������������Գ�������Ϊ4���ĸ�����![]() �����������ֿ����Ƿ���ȷ��˵�����ɣ�
�����������ֿ����Ƿ���ȷ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ϊ������������ȥ��ˮ��羰�����Σ��Ƴ��������շѱ���
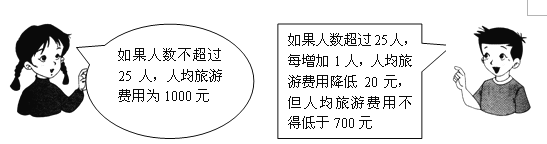 ij��λ��֯Ա��ȥ��ˮ��羰�����Σ���֧�����������������η���27000Ԫ�����ʸõ�λ��ι��ж���Ա��ȥ��ˮ��羰�����Σ�
ij��λ��֯Ա��ȥ��ˮ��羰�����Σ���֧�����������������η���27000Ԫ�����ʸõ�λ��ι��ж���Ա��ȥ��ˮ��羰�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ���Ե�Բ�ĽǷֱ���
���Ե�Բ�ĽǷֱ���![]() ��
��![]() ����
����![]() ��
��![]() ������
������![]() �ij����ڣ� ��
�ij����ڣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ı��ε�ѧϰ�����ǿ��Զ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı�������
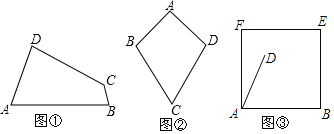
̽������
��1����ͼ�٣���֪�ı���ABCD�����ȶԽ��ı���������A����C����A=70������B=80�������C����D�Ķ�����
��2����ͼ�ڣ���AB=AD=a��CB=CD=b����a��b����ô�ı���ABCD�����ȶԽ��ı���������˵�����ɣ�
����Ӧ��
��3����ͼ�ۣ��ڱ߳�Ϊ6��������ľ��ABEF�ϲó����ȶԽ��ı�����ABCD�����Ѿ�ȷ��DA=4����DAB=60�����Ƿ���������ABEF�ڣ��������ϣ�����һ���C��ʹ�ı���ABCD�ԡ�DAB=��BCDΪ�ȶԽǵ��ı��ε������������ڣ�������ı���ABCD�����������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� x �ĺ��� y=��m��1��x2+2x+m ͼ����������ֻ�� 2 �����㣬��m=_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y��![]() x��˫����y��
x��˫����y��![]() ����A��B���㣬�ҵ�A�ĺ�����Ϊ
����A��B���㣬�ҵ�A�ĺ�����Ϊ![]() ��
��
��1����k��ֵ��
��2����˫����y��![]() �ϵ�C��������Ϊ3�����AOC�������
�ϵ�C��������Ϊ3�����AOC�������
��3��������������һ��M����ֱ��AB����һ��P����˫����y��![]() ����һ��N������O��M��P��NΪ������ı�������һ��Խ�Ϊ60������Σ���д���������������ĵ�P�����꣮
����һ��N������O��M��P��NΪ������ı�������һ��Խ�Ϊ60������Σ���д���������������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com