
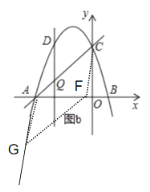
【题目】如图,抛物线![]() 交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
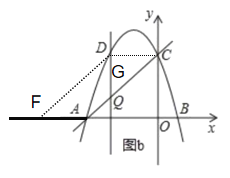
(2)若点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
(3)点G是抛物线上的动点,点F在x轴上的动点,若以A,C,F,G四个点为顶点的四边形是平行四边形,求出所有满足条件的点F坐标(直接写出结果).

【答案】(1)y=-x2-2x+3;(2)QD最大值为![]() ;(3)(-1,0),(-5,0),(
;(3)(-1,0),(-5,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
(1)将点A、C的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答;
(2)利用待定系数法求一次函数解析式求出直线AC的解析式,然后表示出DQ,再根据二次函数的最值问题解答;
(3)设点![]() ,再分情况根据平行四边形的性质求出所有满足条件的点F坐标即可.
,再分情况根据平行四边形的性质求出所有满足条件的点F坐标即可.
将点![]() ,点
,点![]() 代入
代入![]() 得
得
![]()
解得![]()
∴抛物线的函数表达式为![]()
(2)设直线AC的解析式为![]()
则![]()
解得![]()
∴直线AC的解析式为![]() ,
,
![]()
![]()
![]()
![]()
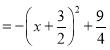
∴当![]() 时,线段DQ长度的最大值为
时,线段DQ长度的最大值为![]()
(3)设点![]() ,
,
①如图,
∵![]() ,点
,点![]() ,点
,点![]()
∴![]()
![]()
解得![]()
∴![]()
∴![]()
∴![]()
②如图,
∵![]() ,点
,点![]() ,点
,点![]()
∴![]()
![]()
解得![]()
∴![]()
∴![]()
∴![]()

③如图,
∵平行四边形对角线互相平分
∴点C和点G的纵坐标之和为0
∵点![]()
∴![]()
![]()
![]()
![]()
解得![]()
当![]() 时,对角线交点坐标为
时,对角线交点坐标为
∴![]()
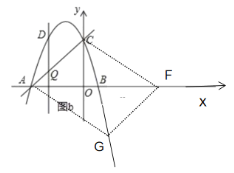
④如图,根据③可得
当![]() 时,对角线交点坐标为
时,对角线交点坐标为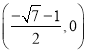
∴![]()
故所有满足条件的点F的坐标为(-1,0),(-5,0),(![]() ,0),(
,0),(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】在长春创建文明城区的活动中,需铺设两段长度相等的彩色道砖,分别交给甲、乙两个施工队同时进行施工.甲、乙两队所铺设彩色道砖的长度![]() (米)与施工时间
(米)与施工时间![]() 时之间的部分函数图象如图所示.请解答下列问题:
时之间的部分函数图象如图所示.请解答下列问题:
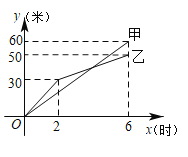
(1)甲队的速度是_______米![]() 时.
时.
(2)当![]() 时,求乙队铺设彩色道砖的长度
时,求乙队铺设彩色道砖的长度![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)如果甲队施工速度不变,乙队在开挖![]() 小时后;施工速度增加到
小时后;施工速度增加到![]() 米
米![]() 时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度.
时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的内接三角形,
的内接三角形,![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() .
.

(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若在![]() 上取一点
上取一点![]() 使
使![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
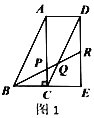
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() ,易得
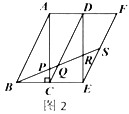
,易得![]() .若取四个直角三角形拼成如图2所示的形状,
.若取四个直角三角形拼成如图2所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 在
在![]() 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从![]() 点出发向
点出发向![]() 点移动,过
点移动,过![]() 作
作![]() 交
交![]() 边于
边于![]() 点,连结
点,连结![]() 、
、![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() .
.
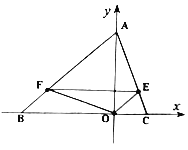
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)计算:当![]() 面积最大时,
面积最大时,![]() 的值;
的值;
(3)在(2)的条件下,边![]() 上是否还存在一个点
上是否还存在一个点![]() ,使得
,使得![]() ?若存在,请直接写出
?若存在,请直接写出![]() 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一笔直的公路连接![]() 、
、![]() 两地,甲车从
两地,甲车从![]() 地驶往
地驶往![]() 地,速度为每小时60千米,同时乙车从
地,速度为每小时60千米,同时乙车从![]() 地驶往
地驶往![]() 地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往
地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往![]() 地.设甲车行驶的时间为
地.设甲车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() .已知
.已知![]() 与
与![]() 的函数关系的部分图像如图所示.
的函数关系的部分图像如图所示.
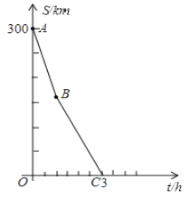
(1)直接写出![]() 点的实际意义.
点的实际意义.
(2)问:甲车出发几小时后发生故障?
(3)将![]() 与
与![]() 的函数图象补充完整.(请对画出的图象用数据作适当的标注)
的函数图象补充完整.(请对画出的图象用数据作适当的标注)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com