
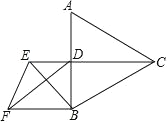
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
【答案】![]()
【解析】
首先证明△CBE≌△ABF,推出∠BAF=∠BCE,由CA=CB,CD⊥AB,推出∠BCE=![]() ∠ACB=30°,AD=BD=4,推出∠BAF=30°=定值,根据垂线段最短可知,当DF⊥AF时,DF的值最小.
∠ACB=30°,AD=BD=4,推出∠BAF=30°=定值,根据垂线段最短可知,当DF⊥AF时,DF的值最小.
如图,
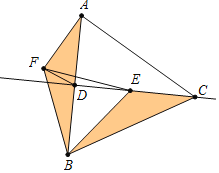
∵△ABC,△BEF的是等边三角形,
∴AB=BC,BF=BE,∠ABC=∠ACB=∠EBF=60°,
∴∠CBE=∠ABF,
在△BCE和△BAF中,
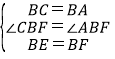 ,
,
∴△CBE≌△ABF(SAS),
∴∠BAF=∠BCE,
∵CA=CB,CD⊥AB,
∴∠BCE=![]() ∠ACB=30°,AD=BD=
∠ACB=30°,AD=BD=![]() ,
,
∴∠BAF=30°是定值,
∴根据垂线段最短可知,当DF⊥AF时,DF的值最小,
∴DF的最小值=![]() AD=
AD=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
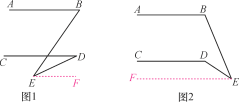
查看答案和解析>>
科目:初中数学 来源: 题型:
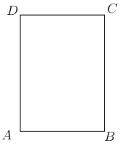
【题目】如图,已知一张长方形纸片,![]() ,
,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() , 则
, 则![]() 等于多少°;
等于多少°;
(3)用含有![]() 、
、![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )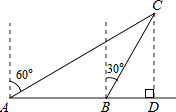
A.20海里
B.40海里
C.20 ![]() 海里
海里
D.40 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值.
(1)(2x2y-4xy2)-(-![]() xy2+x2y),其中x=-1,y=2;
xy2+x2y),其中x=-1,y=2;
(2)2x2-[3(-![]() x2+
x2+![]() xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-
xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-![]() |+(y+1)2=0.
|+(y+1)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有黑球两个,白球三个,这些小球除颜色外无其他区别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是黑球的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
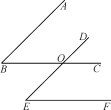
【题目】如图,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为题设,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com