
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
【答案】(1)每台电脑0.5万元,每台电子白板1.5万元;(2)有三种购买方案,方案1:需购进电脑15台,则购进电子白板15台,方案2:需购进电脑16台,则购进电子白板14台,方案3:需购进电脑17台,则购进电子白板13台.选择方案3最省钱,即购买电脑17台,电子白板13台最省钱.
【解析】
试题分析:本题考查了二元一次方程组和一元一次不等式组的应用,解题的关键是读懂题意,找出之间的数量关系,列出二元一次方程组和一元一次不等式组,注意a只能取整数.(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元列出不等式组,求出a的取值范围,再根据a只能取整数,得出购买方案,再根据每台电脑的价格和每台电子白板的价格,算出总费用,再进行比较,即可得出最省钱的方案.
试题解析:(1)设每台电脑x万元,每台电子白板y万元,根据题意得:![]() ,解得:
,解得:![]() ,
,
答:每台电脑0.5万元,每台电子白板1.5万元;
(2)设需购进电脑a台,则购进电子白板(30﹣a)台,根据题意得:![]() ,解得:15≤a≤17,∵a只能取整数,∴a=15,16,17,∴有三种购买方案,方案1:需购进电脑15台,则购进电子白板15台,方案2:需购进电脑16台,则购进电子白板14台,方案3:需购进电脑17台,则购进电子白板13台.方案1:15×0.5+1.5×15=30(万元),方案2:16×0.5+1.5×14=29(万元),方案3:17×0.5+1.5×13=28(万元),∵28<29<30,∴选择方案3最省钱,即购买电脑17台,电子白板13台最省钱.
,解得:15≤a≤17,∵a只能取整数,∴a=15,16,17,∴有三种购买方案,方案1:需购进电脑15台,则购进电子白板15台,方案2:需购进电脑16台,则购进电子白板14台,方案3:需购进电脑17台,则购进电子白板13台.方案1:15×0.5+1.5×15=30(万元),方案2:16×0.5+1.5×14=29(万元),方案3:17×0.5+1.5×13=28(万元),∵28<29<30,∴选择方案3最省钱,即购买电脑17台,电子白板13台最省钱.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如今,优学派电子书包通过将信息技术与传统教学深度结合,让智能科技在现代教育中发挥了重要作用。某优学派公司筹集资金12.8万元,一次性购进两种新型电子书包访问智能终端:平板电脑和PC机共30台.根据市场需要,这些平板电脑、PC机可以全部销售,全部销售后利润不少于1.5万元,其中平板电脑、PC机的进价和售价见如下表格:

设该公司计划购进平板电脑x台,平板电脑和PC机全部销售后该公司获得的利润为y元.
(1) 试写出y与x的函数关系式;
(2) 该公司有哪几种进货方案可供选择?请写出具体方案;
(3) 选择哪种进货方案,该公司获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和频数分布直方图,如图:

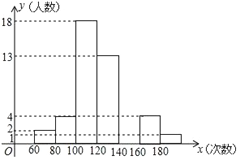
(1)补全频数分布表和频数分布直方图.
(2)表中组距是______次,组数是______组.
(3)跳绳次数在100≤x<140范围的学生有______人,全班共有______人.
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如下表所示:

某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲、乙两班分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
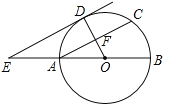
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+x﹣1经过点P(m,5),则代数式m2+m+2018的值为( )
A. 2021B. 2022C. 2023D. 2024
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com