练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，有一只小鸟在一棵高13m的大树树梢上捉虫子，它的伙伴在离该树12m，高为8m的小树树梢上叫它，它立刻以2m/s的速度飞向小树树梢，那么这只小鸟至少要几秒才能飞到伙伴身旁？
    考点：勾股定理的应用
    专题：
    分析：构造直角三角形，利用勾股定理求斜边的值是13m，也就是两树树梢之间的距离是13m，再利用路程除以速度求时间．
    解答：解：如图所示：
    根据题意，得
    AC=AD-BE=13-8=5m，BC=12m．
    根据勾股定理，得
    AB=
    		AC2+BC2
    =13m．
    则小鸟所用的时间是13÷2=6.5（s）．
    答：这只小鸟至少6.5秒才可能到达小树和伙伴在一起．
    点评：此题主要考查勾股定理的运用．关键是构造直角三角形，同时注意：时间=路程÷速度．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    我市雁塔区曾对中考取得优秀成绩的学生就其学习有何诀窍做了一次测试，共300名学生参加了测试，并就“取得优异成绩的关键因素在于什么”发表了自己的看法，其结果如下表
    关键因素自身努力刻苦学习方法科学教师讲解到位自身头脑聪明
    人数（名）150606030
    （1）阅读上表，作出关于“取得优异成绩的关键因素”的扇形统计图；
    （2）我年级某同学上课不认真听讲，放学后经常上网打游戏，抄作业应付老师，导致其经常因成绩不好而被家长责罚．你作为他的同学，请结合上表和所做的统计图中的信息为他提两条合理的建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    （1）x-
    1-x
    3
    =
    x+2
    6
    -1
    （2）2（3y-1）=7（y-2）+3
    （3）|2x-1|=3x+2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

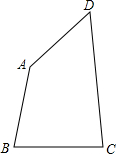    如图，在凸四边形ABCD中，C、D为定点，CD=3，A、B为动点，满足AB=BC=DA=1．
    （Ⅰ）写出cosC与cosA的关系式；
    （Ⅱ）设△BCD和△ABD的面积分别为S和T，求S2+T2的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若函数y=kx+b的图象经过点（0，-1），（-3，2），求k，b的值及函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：（3x+2）2=4（x-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）-14+50÷22×（-
    1
    5
    ）
    （2）0÷（-5）-53-5
    （3）(-
    5
    6
    +
    3
    8
    )×(-24)
    （4）16÷(-2)3-(-
    1
    8
    )×(-4)    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）24×（-5）-（-1）÷
    1
    125
    ；　　　　　　　　　　　　　
    （2）
    7
    9
    ÷|
    1
    5
    -
    2
    3
    |-
    1
    3
    ×（-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

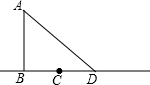    如图，学校旗杆AB的顶端A处挂有一根绳子．小莹在测量旗杆的高度时，先把绳子沿旗杆下垂到点B，固定后再把余下的部分BC拉紧成线段BC（绳子的一端落在C点），然后再将绳子重新拉紧成线段AD（绳子的一端落在D点）．小莹只用卷尺在地面上测量了两个数据，就计算出了旗杆高度，你知道测量了哪两个数据吗？你能求出旗杆的高度吗？

    查看答案和解析>>

    同步练习册答案