Question

已知在△ABC中，AB=3，AC=4，高AD=

12

5

，则S_△ABC=

 

．

Answer 1

考点：勾股定理

专题：

分析：分两种情况：三角形ABC为锐角三角形；三角形ABC为钝角三角形，根据AD垂直于BC，利用垂直的定义得到三角形ABD与三角形ADC为直角三角形，利用勾股定理分别求出BD与DC，由BD+DC=BC或CD-DB=BC求出BC，利用三角形的面积公式即可求出三角形ABC的面积．

解答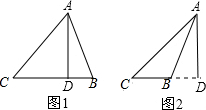：解：分两种情况考虑：
①当△ABC为锐角三角形时，如图1所示，
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
在Rt△ABD中，AB=3，AD=

12

5

，
根据勾股定理得：BD=

AB2-AD2

=

9

5

，
在Rt△ADC中，AC=4，AD=

12

5

，
根据勾股定理得：DC=

AC2-AD2

=

16

5

，
∴BC=BD+DC=5，
则S_△ABC=

1

2

BC•AD=6；
②当△ABC为钝角三角形时，如图2所示，
∵AD⊥BC，
∴∠ADB=90°，
在Rt△ABD中，AB=3，AD=

12

5

，
根据勾股定理得：BD=

AB2-AD2

=

9

5

，
在Rt△ADC中，AC=4，AD=

12

5

，
根据勾股定理得：DC=

AC2-AD2

=

16

5

，
∴BC=CD-BD=

7

5

，
则S_△ABC=

1

2

BC•AD=

42

25

．
综上，△ABC的面积为6或

42

25

．
故答案为：6或

42

25

．

点评：此题主要考查学生对勾股定理和三角形面积等知识点的理解和掌握．解答此题的关键是利用勾股定理分别求出BD和DC的长，此题属于基础题，要求学生熟练掌握．