
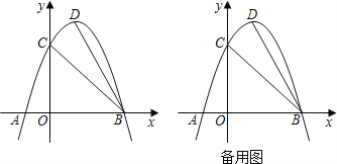
����Ŀ�� ��ͼ��������y=-x2+bx+c��x�ύ��A��B���㣬��y����������C�㣬DΪ�����ߵĶ��㣬A��-1��0����B��3��0����
��1��������κ����ı���ʽ��
��2����P��x���ϣ�����PCB=��CBD�����P�����꣮
��3����x���Ϸ����������Ƿ����һ��Q��ʹ����Q��C��B��OΪ������ı��α��Խ��߷ֳ������ȵ������֣�������ڣ���ֱ��д����Q�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��y=-x2+2x+3����2��P��6��0����P![]() ����3�����ڣ���Q
����3�����ڣ���Q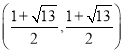 ��
��![]() ��
��
��������
��1������A��B����������ʽ���b��c��ֵ���ɵã�
��2����PCB=��CBD�������������P��B���Ҳ�ʱ���ӳ�BD��y���ڵ�H���ɡ�OCB=��OBC=45������֤����HCB=��CBP���Ӷ���PCB�ա�HBC����ֱ��BD������ã�OH=OP=6���Ӷ��õ�P�����ꣻ��P��B�����ʱ����ʱPC��BD������һ�κ�������ʽ�������P��
��3����������������ֱ���⣬�ٵ�Q��y���Ҳ�ʱ����OB=OC���ɵó�OQ����BOC��ƽ���ߣ��������κ�������ʽ��ֱ��OQ�Ľ���ʽ������⣻�ڵ�Q��y�����ʱ���ɵ������Խ���ֻ����BQ������C��x���ƽ����EF������Q��B�ֱ���EF�Ĵ��ߣ�����ֱ�ΪF��E���ӳ�FQ��x���ڵ�G�����Q������Ϊ(m��n)������S��BOQ=S��CBQ=S����FQBE-S��FCQ-S��BEC�ɵó�����m��n�Ĺ�ϵʽ��������κ����Ľ���ʽ����������⣮
�⣺��1������A��-1��0����B��3��0������y=-x2+bx+c�ã�
![]() �����
�����![]() ��
��
����κ����ı���ʽΪy=-x2+2x+3��
��2���ٵ���P�ڵ�B�Ҳ�ʱ���ӳ�BD��y���ڵ�H��

��y=-x2+2x+3=-��x-1��2+4�����D��������1��4����
��ֱ��BD�Ľ���ʽΪy=kx+b����
![]() �����
�����![]() ����ֱ��BD�Ľ���ʽΪy=-2x+6��
����ֱ��BD�Ľ���ʽΪy=-2x+6��
���H��������0��6����
��OB=OC=3�����OBC=��OCB=45����
���HCB=��CBP=135����
�֡�PCB=��CBD��BC=BC��
���PCB�ա�HBC��
��CH=PB��
��OH=OB=6��
�ʴ�ʱ��P������Ϊ��6��0����
�ڵ���P��P�����ڵ�B���ʱ��
ֱ��BD�ı���ʽΪ��y=-2x+6��
�ߡ�P��CB=��CBD����P��C��BD��
��ֱ��P��C�ı���ʽΪ��y=-2x+3��
��y=0��x=![]() ���ʴ�ʱ��P��������Ϊ
���ʴ�ʱ��P��������Ϊ![]() ��
��
������������P��������6��0����![]() ��
��
��3�����ڣ��������£�������Q��y���Ҳ�ʱ����Q��C��B��OΪ������ı��α��Խ��߷ֳ������ȵ������֣������Խ���ֻ����OQ��S��COQ=S��BOQ����ͼ��
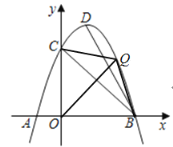
��OB=OC����OQ�ǡ�BOC��ƽ���ߣ�
��OQ�ĺ�������ʽΪ��y=x��
��y=x��y=-x2+2x+3�����ã�
-x2+2x+3=x�����x=![]() ����ȥ��ֵ����
����ȥ��ֵ����
�ʴ�ʱ��Q������Ϊ��![]() ��
��![]() ����
����
������Q��y�����ʱ����Q��C��B��OΪ������ı��α��Խ��߷ֳ������ȵ������֣������Խ���ֻ����BQ��S��BOQ=S��CBQ����ͼ������C��x���ƽ����EF������Q��B�ֱ���EF�Ĵ��ߣ�����ֱ�ΪF��E���ӳ�FQ��x���ڵ�G����QG��x�ᣬBE=CO=3=FG��BO=CE=3��
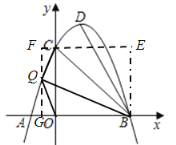
���Q������Ϊ(m��n)����QG=n��FQ=3-n��OG=FC=-m��
��S��BOQ=![]() ��3��n��
��3��n��
S��CBQ=S����FQBE-S��FCQ-S��BEC=![]() ����3-n+3������3-m��-
����3-n+3������3-m��-![]() ��(-m)��(3-n)-
��(-m)��(3-n)-![]() ��3��3=
��3��3=![]() (9-3m-3n)��
(9-3m-3n)��
��![]() ��3��n
��3��n![]() (9-3m-3n)����m+2n=3�٣�
(9-3m-3n)����m+2n=3�٣�
�ֵ�Q�ڶ��κ���ͼ���ϵã�n=-m2+2m+3�ڣ�
�����٢ڵã�![]() �����
����� ��
��![]() ��ȥ����
��ȥ����
���Q��������-![]() ��
��![]() ����
����
������������Q������Ϊ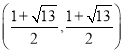 ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
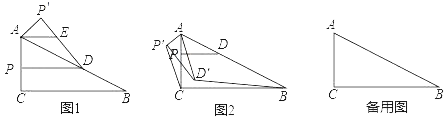
����Ŀ��Rt��ABC�У���ACB��90����AC��3��BC��7����P�DZ�AC�ϲ����A��C�غϵ�һ�㣬��PD��BC��AB���ڵ�D��
��1����ͼ1������APD��ֱ��AB���ۣ��õ���AP'D����AE��PD����֤��AE��ED��
��2������APD�Ƶ�A˳ʱ����ת���õ���AP'D'����P��D�Ķ�Ӧ��ֱ�Ϊ��P'��D'��
����ͼ2������D'����ABC�ڲ�ʱ������P��C��D'B����֤����AP'C�ס�AD'B��
�����AP��PC��5��1������DD'����DD'��![]() AD����ô��ֱ��д����D'��ֱ��BC�ľ��룮
AD����ô��ֱ��д����D'��ֱ��BC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
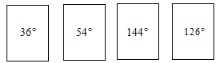
����Ŀ����ͼ���������ʵ���ȫ��ͬ�Ŀ�Ƭ������ֱ�д���ĸ��Ƕȣ��ֽ������ſ�Ƭϴ�Ⱥ��泯�ϣ�
(1)�����������ȡ--�ţ���鵽��ǿ�Ƭ�ĸ��ף�
(2)�����������ȡ���ţ���鵽�����ŽǶ�ǡ�û����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
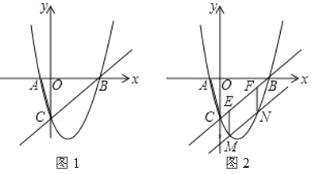
����Ŀ����ͼ1�����κ���y��ax2��3ax��4a��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C(0����3)��
��1������κ����ı���ʽ����A����B�����ꣻ
��2������D�ڶ��κ���ͼ���ϣ���![]() �����D�ĺ����ꣻ
�����D�ĺ����ꣻ
��3����ֱ��BC����ƽ�ƣ�����κ���ͼ����M��N���㣨M��N��ࣩ����ͼ2����M��ME��y�ᣬ��ֱ��BC���ڵ�E����N��NF��y�ᣬ��ֱ��BC���ڵ�F����MN+ME��ֵ���ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
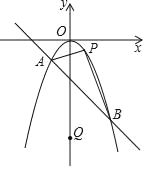
����Ŀ����ͼ��ʾ����֪������y��ax2��a��0����һ�κ���y��kx+b��ͼ���ཻ��A����1����1����B��2����4�����㣬��P���������ϲ���A��B�غϵ�һ�����㣬��Q��y���ϵ�һ�����㣮
��1����ֱ��д��a��k��b��ֵ������x�IJ���ʽax2��kx��2�Ľ⼯��
��2������P��ֱ��AB�Ϸ�ʱ���������PAB��������ֵ�������ʱ��P�����ꣻ
��3���Ƿ������P��Q��A��BΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��P��Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı��� ABCD �У��Խ��� AC��BD �ཻ�ڵ� O������ O ������ֱ�߷ֱ� AB��CD��AD��BC �ڵ� E��F��G��H��
����֪����ͼ�������ı��� ABCD �������Σ��� AG��BE��CH��DF���� S �ı���AEOG�� S ������ ABCD��
����չ����ͼ�ڣ����ı��� ABCD �Ǿ������� S �ı��� AEOG��![]() S ���� ABCD���� AB��a�� AD��b��BE��m���� AG �ij����ú� a��b��m �Ĵ���ʽ��ʾ����
S ���� ABCD���� AB��a�� AD��b��BE��m���� AG �ij����ú� a��b��m �Ĵ���ʽ��ʾ����
��̽������ͼ�������ı��� ABCD ��ƽ���ı��Σ��� AB��3��AD��5��BE��1�� ��ȷ�� F��G��H ��λ�ã�ʹֱ�� EF��GH ���ı��� ABCD ������ĵȷ֣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����A����2��6��������x���ཻ�ڵ�B��������������y=3x��ͼ���ཻ�ڵ�C����C�ĺ�����Ϊ1��
��1����k��b��ֵ��
��2������D��y�Ḻ�����ϣ�������S��COD=![]() S��BOC�����D�����꣮
S��BOC�����D�����꣮
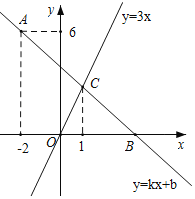
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�������ۡ�C��ʹ��C����б��AB��ijһ��D�����ۺ�ΪEF����E��F�ֱ��ڱ�AC��BC�ϣ������������жϣ��ٵ�CD��ABʱ��EFΪ��ABC����λ�ߣ��ڵ��ı���CEDFΪ����ʱ��AC��BC���۵���DΪAB���е�ʱ����CEF���ABC���ƣ��ܵ���CEF���ABC����ʱ����DΪAB���е㣮������ȷ����_____����������ȷ�Ľ��۵���Ŷ����ں����ϣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�мƻ���ʮ������ͨ�����ⷿ���裬�����������Ⱥ��ס�����⣮��֪ǰ7�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף���ʱ��x����x�꣩�Ĺ�ϵ����һ�κ�����1��x��7��xΪ���������ҵ�һ�͵����꿢��Ͷ��ʹ�õĹ��ⷿ����ֱ�Ϊ![]() ��
��![]() ����ƽ���ף���5��ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף���ʱ��x����x�꣩�Ĺ�ϵ��y=��
����ƽ���ף���5��ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף���ʱ��x����x�꣩�Ĺ�ϵ��y=��![]() x+
x+![]() ��7��x��12��x��������
��7��x��12��x��������
��1����֪��6�꿢��Ͷ��ʹ�õĹ��ⷿ����ɽ��20���˵�ס�����⣬����˾�ס����������һ��Ҫ�ȵ�6�����20%����ô���һ�꿢��Ͷ��ʹ�õĹ��ⷿ����ɽ���������˵�ס�����⣿
��2����������ǵ����ص�Ӱ�죬��֪��12���У�ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ����������ͬ���ҵ�һ�꣬һ��38Ԫ/m2���ڶ��꣬һ��40Ԫ/m2�������꣬һ��42Ԫ/m2�������꣬һ��44Ԫ/m2�����Դ����ƣ�����˵��ÿƽ����������ʱ���ܷɺ���������ܣ�ֱ��д����������ʽ��
��3���ڣ�2���������£�����ÿ��Ĺ��ⷿ����ȫ�������꣬д����12����ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ�������W����ʱ��x�ĺ�������ʽ�������W�����ֵ����λ����Ԫ���������Wȡ�����ֵ����һ�꣬����������58m2�ķ��ӣ�����������һ��Ӧ���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com