

分析 (1)证明△BFC≌△CHA,得BF=CH,由此可得BF=AH+FH;
(2)证明△AHD≌△DFC可得DH=DF,在证明∠FDH=90°,由此可知△FDH为等腰直角三角形;
(3)证明△BFE≌△CHM即可.
解答 解:(1)∵BF⊥CE于点F,交CD于点G,AH⊥CE于点H,
∴∠ACH=∠CFB=90°.
∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°,
又∠HAE=∠FBE,∠AEH=∠FEB,
∴∠HAE=∠EBF,
又∵∠ACE+∠HAE=∠EBF+∠FBC=45°,
∴∠ACH=∠CBF.
在△BFC和△CHA中,$\left\{\begin{array}{l}{∠BFG=∠CHA}\\{∠ACH=∠CBF}\\{AC=BC}\end{array}\right.$
∴△BFC≌△CHA(AAS)
∴BF=CH,CF=AH,
∵CH=CF+FH,
∴BF=AH+FH
即:线段BF,AH,FH的关系为:BF=AH+FH
(2)△FDH为等腰直角三角形,理由:
∵在Rt△CDE和Rt△BFE中,∠CED=∠BEF
∴∠FBE=∠DCE,
即:∠HAD=∠FCD.
在△AHD和△DFC中,$\left\{\begin{array}{l}{AD=CD}\\{∠FCD=∠HAD}\\{CH=CF}\end{array}\right.$
∴△AHD≌△DFC(SAS)
∴HD=DF
又∵∠CDF+∠FDE=90°,
∴∠FDE=∠EDH=90°,
即:∠FDH=90°,
∴△FDH为等腰直角三角形.
(3)由(1)可知,BF=CH,∠HCM=∠FBE,
在△BFE与△CHM中,$\left\{\begin{array}{l}{∠HCM=∠FBE}\\{BF=CH}\\{∠CHM=∠BFE=90°}\end{array}\right.$
∴△BFE≌△CHM(ASA),
∴BE=CM.
点评 本题考查了三角形全等的判定,解题的关键是把所求等量关系转化为证明相应的三角形全等.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | x≤0,y≠0 | B. | x≤0,y为一切实数 | C. | x<0,y≠0 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.| a | 1 | 2 | 3 |
| s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是矩形,E、F分别是AB、CD的中点,现将矩形的一角沿过点B的折痕BM对折,使得点A落在线段EF上,记为N,则:
如图,四边形ABCD是矩形,E、F分别是AB、CD的中点,现将矩形的一角沿过点B的折痕BM对折,使得点A落在线段EF上,记为N,则:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
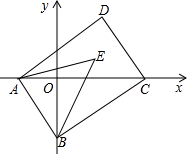 如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:
如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解某校七年级学生完成数学课前预习的惰况,随机抽取该年级100名学生进行了调查,调查结果分为四类:
为了了解某校七年级学生完成数学课前预习的惰况,随机抽取该年级100名学生进行了调查,调查结果分为四类:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 关于x的一元二次方程a2x2+2ax-3=0(a≠0).
关于x的一元二次方程a2x2+2ax-3=0(a≠0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com