
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
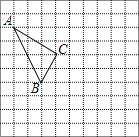
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两个数也互为相反数”
(1)举一个具体的例子来判断上述结论是否成立;
(2)若![]() 和
和![]() 互为相反数,且x+5的平方根是它本身,求x+y的立方根.
互为相反数,且x+5的平方根是它本身,求x+y的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a c b ,那么我们规定(a,b)=c,例如:因为23 8 ,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)= ,(4,1)= ,(2,![]() )= ;
)= ;
(2)若记(3,5)=a,(3,6)=b,(3,30)=c,求证: a b c .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.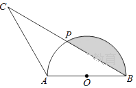
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°,①求弦BP的长;②求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习多项式乘以多项式时发现:(![]() x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:![]() x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(![]() x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.
(1)当∠OAB=40°时,∠ACB= 度;
(2)随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.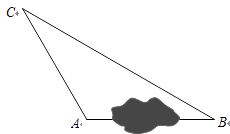
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左石两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,求小巷有多宽.
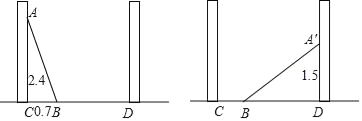
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com