
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
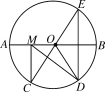
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据弧AC=弧CD=弧DB和点E是点D关于AB的对称点,求出∠DOB=∠COD=∠BOE=60°,求出∠CED,即可判断①②;根据圆周角定理求出M和A重合时,∠MDE=60°,即可判断③;根据轴对称的性质,求出M的位置,根据圆周角定理求出此时CE为直径,即可得到CE的长,判断④.
∵弧AC=弧CD=弧DB,
∴∠DOB=∠COD=∠BOE=60°,
故①正确;
∵AB为直径,且点E是点D关于AB的对称点
∴∠E=∠D,AB⊥DE
∴∠CED=![]() ∠DOB=30°,
∠DOB=30°,
故②正确;
∵M和A重合时,∠MDE=60°,
∴∠MDE+∠E=90°
∴DM⊥CE
故③不正确;
根据轴对称的性质,可知D与E对称,连接CE,根据两点之间线段最短,可知这时的CM+DM最短,
∵∠DOB=∠COD=∠BOE=60°
∴CE为直径,即CE=10,
故④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图,并且C的对应点C′的坐标为(4,1)。
(1)A′、B′.两点的坐标分别为A′ 、B′ ;
(2)请作出△ABC平移之后的图形△A′B′C′;

(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“重百”、“沃尔玛”两家超市出售同样的保温壶和水杯,保温壶和水杯在两家超市的售价分别一样.已知买1个保温壶和1个水杯要花费60元,买2个保温壶和3个水杯要花费130元.
(1)请问:一个保温壶与一个水杯售价各是多少元;(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“重百”超市规定:这两种商品都打九折;“沃尔玛”超市规定:买一个保温壶赠送一个水杯.若某单位想要买4个保温壶和15个水杯,如果只能在一家超市购买,请问选择哪家超市购买更合算,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
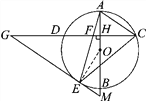
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.
上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
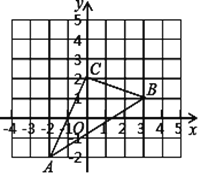
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在△ABC中,AC=BC,∠ ACB=90°,AD平分∠BAC交BC边于点D,过B 作BH⊥AD,交AC的延长线于点E,H为垂足.
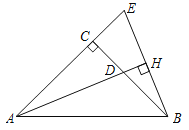
(1)求证: △ACD ≌ △BCE;
(2)找出BH和BC有怎样的数量关系(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com