
【题目】已知二次函数y=![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(Ⅰ)求这个二次函数的解析式;
(Ⅱ)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(Ⅲ)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
【答案】(Ⅰ)二次函数解析式为y=![]() x2﹣x﹣
x2﹣x﹣![]() ;(Ⅱ)△DCP是等腰直角三角形,理由见解析;(Ⅲ)点Q坐标为(5,6).
;(Ⅱ)△DCP是等腰直角三角形,理由见解析;(Ⅲ)点Q坐标为(5,6).
【解析】
(Ⅰ)把A(-3,6),B(-1,0)代入y=![]() x2+bx+c,解方程组即可解决问题.
x2+bx+c,解方程组即可解决问题.
(Ⅱ)结论:△DCP是等腰直角三角形.求出C、D、E三点坐标即可解决问题.
(Ⅲ)如图,连接BE、DE.只要证明△EOB≌△EOD,得到∠DEO=∠BEO,所以直线DE与抛物线的交点即为所求的点Q.求出直线DE的解析式,解方程组即可.
(Ⅰ)把A(﹣3,6),B(﹣1,0)代入y=![]() x2+bx+c,
x2+bx+c,
得到 ,
,
解得 ,
,
∴二次函数解析式为y=![]() x2﹣x﹣
x2﹣x﹣![]() .
.
(Ⅱ)结论:△DCP是等腰直角三角形.
理由:对于抛物线y=![]() x2﹣x﹣
x2﹣x﹣![]() ,令y=0,则
,令y=0,则![]() x2﹣x﹣
x2﹣x﹣![]() =0,解得x=﹣1或3,
=0,解得x=﹣1或3,
∴点C坐标(3,0),
令x=0则y=﹣![]() ,
,
∴点E坐标(0,﹣![]() ),
),
∵y=![]() x2﹣x﹣
x2﹣x﹣![]() =
=![]() (x﹣1)2﹣2,
(x﹣1)2﹣2,
∴顶点P坐标(1,﹣2),点D坐标(1,0),
∴CD=PD=2,
∵∠PDC=90°,
∴△PDC是等腰直角三角形.
(Ⅲ)如图,连接BE、DE.

∵B(﹣1,0),D(1,0),E(0,﹣![]() ),
),
∴OB=OD,OE=OE,∠BOE=∠DOE,
∴△EOB≌△EOD,
∴∠DEO=∠BEO,
∴直线DE与抛物线的交点即为所求的点Q.
设直线DE的解析式为y=kx+b,则有 ,
,
解得 ,
,
∴直线DE的解析式为y=![]() ,
,
由 解得
解得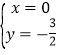 或
或![]() ,
,
∴点Q坐标为(5,6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
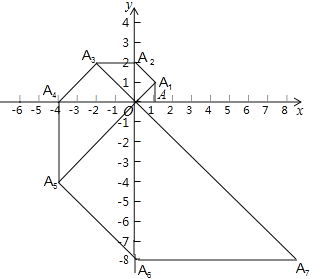
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2019的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
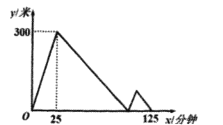
【题目】“龟、蟹赛跑趣事”:某天,乌龟和螃蟹在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑500米。当螃蟹领先乌龟300米时,螃蟹停下来休息并睡着了,当乌龟追上螃蟹的瞬间,螃蟹惊醒了(惊醒时间忽略不计)并立即以原来的速度继续跑向终点,并赢得了比赛。在比赛的整个过程中,乌龟和螃蟹的距离![]() (米)与乌龟出发的时间
(米)与乌龟出发的时间![]() (分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
(分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点C开始沿边CB向终点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,当点Q运动到点B时,两点停止运动.设运动时间为t秒.

(1)填空:BQ=______________cm,PB=_______________cm(用含t的代数式表示);
(2)当t为何值时,PQ的长度等于![]() cm?
cm?
(3)是否存在t的值,使得五边形APQCD的面积等于27![]() ?若存在,请求出此时t的值;若不存在,请说明理由
?若存在,请求出此时t的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按指定的方法解下列方程:
(1)2x2-5x-4=0(配方法);
(2)3(x-2)+x2-2x=0(因式分解法);
(3)(a2-b2)x2-4abx=a2-b2(a2≠b2)(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com