
【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 , 它(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
【答案】
(1)123123,能
(2)解:任意六位连接数都能被13整除,理由如下:
设 ![]() 为六位连接数,
为六位连接数,
∵ ![]() =
= ![]() ×1001=
×1001= ![]() ×13×77,
×13×77,
∴ ![]() 能被13整除
能被13整除
(3)解:设 ![]() 为四位连接数,
为四位连接数,
则M=1000x+100y+10x+y=1010x+101y,N=3(x+y+x+y)=6x+6y,
∴M﹣N=(1010x+101y)﹣(6x+6y)=1004x+95y,
∴ ![]() =
= ![]() =77x+7y+
=77x+7y+ ![]() ,
,
∵M﹣N的结果能被13整除,
∴ ![]() 是整数,
是整数,
∵M与N都是1~9之间的整数,
∴x=1,y=9;x=2,y=5;x=3,y=1;
∴这样的四位连接数有1919,2525,3131,一共3个.
【解析】解:(1)123123为六位连接数;
∵123123=123×1001=123×13×77,
∴123123能被13整除;
【考点精析】利用因式分解的应用对题目进行判断即可得到答案,需要熟知因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.


科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 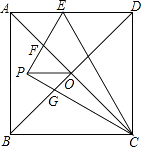
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时,![]() 有最小值10;②
有最小值10;②![]() 为任意实数,
为任意实数,![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时,![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,其中
,其中![]() ,
,![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.① B.② C.③ D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:

(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com