
【题目】如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是( )

①图甲,DE⊥AC,BF⊥AC
②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点
④图丁,E是AB上一点,EF⊥AB.
A. 3个B. 4个C. 1个D. 2个
【答案】A
【解析】
①由DE⊥AC,BF⊥AC,可得DE∥BF,又由四边形ABCD是平行四边形,利用△ACD与△ACB的面积相等,即可判定DE=BF,然后由一组对边平行且相等的四边形是平行四边形,证得四边形BFDE是平行四边形;
②由四边形ABCD是平行四边形,DE平分∠ADC,BF平分∠ABC,易证得△ADE≌△CBF,则可判定DE∥BF,DE=BF,继而证得四边形BFDE是平行四边形;
③由四边形ABCD是平行四边形,E是AB的中点,F是CD的中点,易证得DF∥BE,DF=BE,继而证得四边形BFDE是平行四边形;
④无法确定DF=BE,只能证得DF∥BE,故不能判定四边形BFDE是平行四边形.
解:①∵四边形ABCD是平行四边形,
∴S△ACD=S△ABC,
∵DE⊥AC,BF⊥AC,
∴DE∥BF,S△ACD=![]() ACDE,S△ABC=
ACDE,S△ABC=![]() ACBF,
ACBF,
∴DE=BF,
∴四边形BFDE是平行四边形;
②∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=CB,AD∥BC,
∴∠DAE=∠BCF,
∵DE平分∠ADC,BF平分∠ABC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
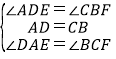 ,
,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形BFDE是平行四边形;
③证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB的中点,F是CD的中点,
∴DF=![]() CD,BE=
CD,BE=![]() AB,
AB,
∴DF=BE,
∴四边形BFDE是平行四边形;
④∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB上一点,EF⊥AB,
无法判定DF=BE,
∴四边形BFDE不一定是平行四边形.
故选:A.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 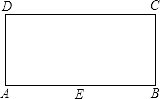
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在招商引资期间,把已经破产的油泵厂出租给外地某投资商,该投资商为了减少固定资产投资,将原来400平方米的正方形场地建成300平方米的长方形场地,并且长、宽的比为5:3,并且把原来的正方形铁栅栏围墙全部利用,围成新场地的长方形围墙,请问这些铁栅栏是否够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 , x2 , 且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AD是BC边上的中线,有以下结论:①AD平分∠BAC;②△ABD的周长-△ACD的周长=AB-AC;③BC=2AD;④△ABD的面积是△ABC面积的一半.其中正确的是( )

A.①②④B.②③④C.②④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com