
 已知:在如图的平面直角坐标系中,△ABC三个顶点坐标分别为A(-2,-1),B(-5,0),C(-2,4).
已知:在如图的平面直角坐标系中,△ABC三个顶点坐标分别为A(-2,-1),B(-5,0),C(-2,4).科目:初中数学 来源: 题型:
 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
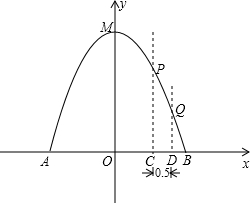
 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:

| 多面体 | 面数a | 展开图的顶点数b | 展开图的棱数c |
| 直三棱柱 | 5 | 10 | 14 |
| 四棱锥 | 5 5 |
8 | 12 |
| 立方体 | 6 6 |
14 14 |
19 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
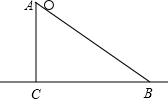 在地面上有一个斜坡装置(如图),已知斜坡的铅直高度AC=0.6m,水平距离BC=0.8m,小球从顶端A由静止自由下滑,速度均匀增大,0.2s滑至底端B后,继续在平地上滑行15米停止.
在地面上有一个斜坡装置(如图),已知斜坡的铅直高度AC=0.6m,水平距离BC=0.8m,小球从顶端A由静止自由下滑,速度均匀增大,0.2s滑至底端B后,继续在平地上滑行15米停止.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com