
分析 (1)先提取公因式,再用平方差公式分解即可;
(2)先用平方差公式,再用完全平方公式分解即可;
(3)先用乘法公式展开,再合并,最后用平方差公式分解即可;
(3)先用乘法公式展开,再提取公因式,最后用完全平方公式和平方差公式分解即可;
解答 解:(1)3x-12x3=3x(1-4x2)=3x(1-2x)(1+2x),
(2)(x2+4)2-16x2=(x2+4+4x)(x2+4-4x)=(x+2)2(x-2)2,
(3)y(y+4)-4(y+1)=y2+4y-4y-4=(y+2)(y-2)
(4)$2({x^2}-\frac{1}{2})-{x^4}$=2x2-1-x4=-(x4-2x2+1)=-(x2-1)2=-(x+1)2(x-1)2
点评 此题是提公因式和公式法的综合运用,主要考查了提取公因式分解因式和平方差公式,完全平方公式分解因式的方法,解本题的关键是分解因式的方法得选择.


科目:初中数学 来源: 题型:解答题
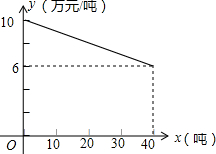 某工厂生产一种产品,当生产数量不超过40吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系式如图所示:
某工厂生产一种产品,当生产数量不超过40吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系式如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com