
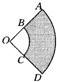
 21、如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB,DC重合,则所围成的几何体图形是( )
21、如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB,DC重合,则所围成的几何体图形是( )科目:初中数学 来源:中学教材全解 七年级数学下 (北京师大版) 北京师大版 题型:044
“抛阶砖”是游戏场的典型游戏之一.如图(1),参与者只需将手上的“金币”抛落身边若干距离的阶砖平面上,抛出的硬币刚巧落在任何一个阶砖的范围内(不与阶砖相连的线重叠),便可获奖.要注意“金币”与阶砖的相对大小将会决定成功抛中阶砖的机会.由于阶砖是正方形,可设每边长度为a,金币的直径为d.若“金币”成功落在阶砖上,它的圆心必位于图(2)的阴影部分内,即“成功”部分是边长为(a-d)的正方形.
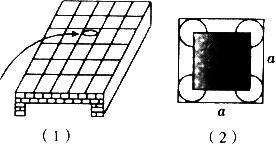
(1)计算“金币”抛落在阶砖范围内的概率(用含a、d的式子表示,0<d<a);
(2)通过配搭“金币”与阶砖之间的大小的设计,做这个“抛阶砖”的游戏,并作好记录,你发现什么规律?
查看答案和解析>>
科目:初中数学 来源:2008年浙江省义乌市初中毕业升学统一考试、数学考试 题型:044
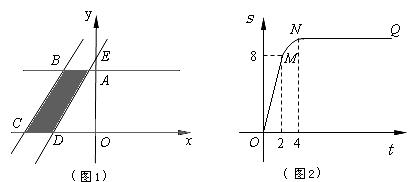
如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部份)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
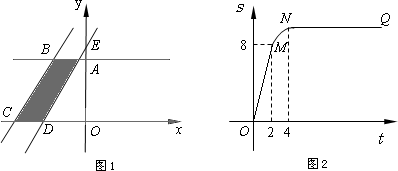
查看答案和解析>>
科目:初中数学 来源:浙江省中考真题 题型:解答题
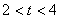 时,求S关于t的函数解析式;
时,求S关于t的函数解析式;查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
 。将直线
。将直线 平移,平移后的直线
平移,平移后的直线 与x轴交于点D,与y轴交于点E。
与x轴交于点D,与y轴交于点E。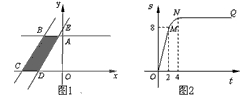
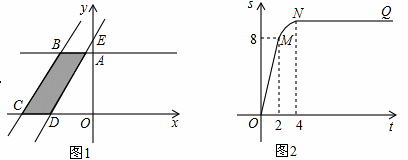
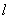 向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线扫过的面积(图中阴影部份)为S,S关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4。
向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线扫过的面积(图中阴影部份)为S,S关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4。 时,求S关于t的函数解析式;
时,求S关于t的函数解析式; 向左或向右平移时(包括
向左或向右平移时(包括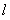 与直线BC重合),在直线AB上是否存在点P,使
与直线BC重合),在直线AB上是否存在点P,使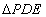 为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由。
为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由。查看答案和解析>>
科目:初中数学 来源: 题型:
如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与![]() 轴负半轴上.过点B、C作直线
轴负半轴上.过点B、C作直线![]() .将直线
.将直线![]() 平移,平移后的直线
平移,平移后的直线![]() 与
与![]() 轴交于点D,与
轴交于点D,与![]() 轴交于点E.
轴交于点E.
(1)将直线![]() 向右平移,设平移距离CD为
向右平移,设平移距离CD为![]() (t
(t![]() 0),直角梯形OABC被直线
0),直角梯形OABC被直线![]() 扫过的面积(图中阴影部份)为
扫过的面积(图中阴影部份)为![]() ,
,![]() 关于
关于![]() 的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当![]() 时,求S关于
时,求S关于![]() 的函数解析式;
的函数解析式;
(2)在第(1)题的条件下,当直线![]() 向左或向右平移时(包括
向左或向右平移时(包括![]() 与直线BC重合),在直线AB上是否存在点P,使
与直线BC重合),在直线AB上是否存在点P,使![]() 为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com