
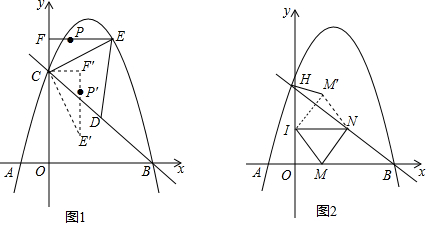
分析 (1)先令y=0和x=0分别求抛物线与x轴和y轴的交点A、B、C的坐标,利用待定系数法求直线BC的解析式;
(2)如图1,根据△CDE中CD是定值,作高线EG,则EG最大时,面积最大,作BC的平行线l,当直线l与抛物线有一个交点时,即△=0时,求E的坐标,并求出此时△CDE面积;
根据垂线段最短和两点之间线段最短,可知:Q从P到F′的最短路径是:延长E′F′交EF于P,确定P点后,再根据两点之间线段最短可知:F′到C是走线段F′C,C到P′是走线段CP′,最后计算其和即可;
(3)当△M′HN为等腰三角形时,分三种情况讨论,分别建立方程计算即可.
解答 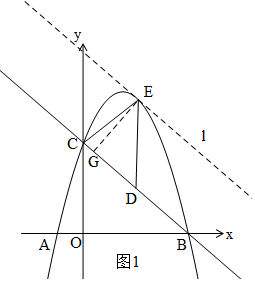 解:(1)当y=0时,-$\frac{\sqrt{3}}{2}$x2+$\frac{3\sqrt{3}}{2}$x+2$\sqrt{3}$=0,
解:(1)当y=0时,-$\frac{\sqrt{3}}{2}$x2+$\frac{3\sqrt{3}}{2}$x+2$\sqrt{3}$=0,
解得x=4或-1,
∵点A在点B的左侧,
∴A(-1,0),B(4,0),
当x=0时,y=2$\sqrt{3}$,
∴C(0,2$\sqrt{3}$),
设直线BC的解析式为:y=kx+b,
把B(4,0)和C(0,2$\sqrt{3}$)代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=2\sqrt{3}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{2}}\\{b=2\sqrt{3}}\end{array}\right.$,
∴直线BC的解析式为:y=-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$;
(2)∵直线BC一定,点D是线段BC中点,
∴CD是定值,
过E作EG⊥CD于G,则当EG最大时,△CDE面积有最大值,
在BC的上方,作直线BC的平行线l,当直线l与抛物线有一个交点时,则交点为E,此时,△CDE面积最大,
设直线l:y=-$\frac{\sqrt{3}}{2}$x+n,
则$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{2}x+n}\\{y=-\frac{\sqrt{3}}{2}{x}^{2}+\frac{3\sqrt{3}}{2}x+2\sqrt{3}}\end{array}\right.$,
-$\frac{\sqrt{3}}{2}{x}^{2}+\frac{3\sqrt{3}}{2}x+2\sqrt{3}$=-$\frac{\sqrt{3}}{2}$x+n,
-$\frac{\sqrt{3}}{2}{x}^{2}$+2$\sqrt{3}$x+2$\sqrt{3}$-n=0,
△=$(2\sqrt{3})^{2}$-4×$(-\frac{\sqrt{3}}{2})$$(2\sqrt{3}-n)$=0,
12+2$\sqrt{3}$($2\sqrt{3}-n$)=0,
24=2$\sqrt{3}$n,
n=4$\sqrt{3}$,
-$\frac{\sqrt{3}}{2}{x}^{2}$+2$\sqrt{3}$x+2$\sqrt{3}$-4$\sqrt{3}$=0,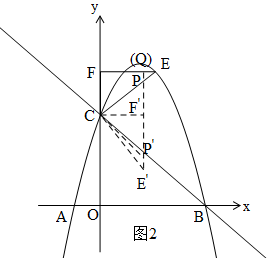
x2-4x+4=0,
x1=x2=2,
∴E(2,3$\sqrt{3}$),
∵点D是线段BC中点,
∴D(2,$\sqrt{3}$),
∴DE⊥x轴,且DE=3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$,
此时,S△DCE=$\frac{1}{2}$DE•xD=$\frac{1}{2}$×$2\sqrt{3}×2$=2$\sqrt{3}$;
∵C(0,2$\sqrt{3}$),E(2,3$\sqrt{3}$),EF⊥y轴,
∴CF=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$,EF=2,
由旋转得:CF′=CF=$\sqrt{3}$,E′F′=EF=2,
当F′P⊥EF时,PF′最短,即E′P⊥EF,E′、F′、P共线,
∴F′P=CF=$\sqrt{3}$,FP=CF′=F′P′=$\sqrt{3}$,
由勾股定理得:CP′=$\sqrt{CF{′}^{2}+F′P{′}^{2}}$=$\sqrt{(\sqrt{3})^{2}+(\sqrt{3})^{2}}$=$\sqrt{6}$,
∴点Q的最短路径是:PF′+F′C+CP′=$\sqrt{3}$+$\sqrt{3}$+$\sqrt{6}$=2$\sqrt{3}$+$\sqrt{6}$;
则△CDE面积的最大值是2$\sqrt{3}$,点Q经过的最短路径的长为2$\sqrt{3}$+$\sqrt{6}$;
(3)由题意得:OM=t,BN=2t,则BM=4-t,HN=5-2t
分三种情况:
①当HN=NM′时,如图3,
由折叠得:NM′=NM,
过N作ND⊥x轴于D,连接MM′,则IN是MM′的中垂线,
sin∠HBO=$\frac{ND}{NB}=\frac{OH}{BH}$,
∴$\frac{ND}{2t}=\frac{3}{5}$,
∴ND=$\frac{6t}{5}$,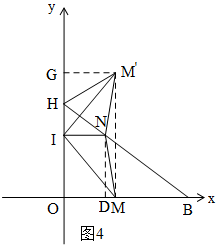
同理得:BD=$\frac{8t}{5}$,
∴DM=BD-BM=$\frac{8t}{5}$-(4-t)=$\frac{13}{5}t$-4,
∵HN=NM,
∴$(5-2t)^{2}=(\frac{6}{5}t)^{2}+(\frac{13}{5}t-4)^{2}$,
21t2-4t-45=0,
t1=$\frac{2+\sqrt{949}}{21}$,t2=$\frac{2-\sqrt{949}}{21}$(舍);
②当HN=HM′时,如图4,过M′作M′G⊥y轴于G,
由①得:OG=MM′=2DN=$\frac{12}{5}t$,OM=M′G=m,
∴GH=$\frac{12t}{5}$-3,
在Rt△GHM′中,M′G2+GH2=M′H2,
∴t2+$(\frac{12}{5}t-3)^{2}$=(5-2t)2,
69t2+140t-400=0,
t1=$\frac{-70-50\sqrt{13}}{69}$(舍),t2=$\frac{-70+50\sqrt{13}}{69}$,
③当M′H=M′N时,如图5,
同理得:HM′=M′N=MN,
在Rt△HGM′和Rt△DNM中,GH2+GM′2=DM2+DN2,
∴t2+$(\frac{12}{5}t-3)^{2}$=$(\frac{6}{5}t)^{2}$+$(\frac{13}{5}t-4)^{2}$,
36t2-160t+175=0,
(2t-5)(18t-35)=0,
t1=$\frac{5}{2}$(舍),t2=$\frac{35}{18}$,
综上所述,当△M′HN为等腰三角形时,t的值是$\frac{2+\sqrt{949}}{21}$或$\frac{-70+50\sqrt{13}}{69}$或$\frac{35}{18}$.
点评 本题是二次函数的综合题,考查了抛物线与坐标轴的交点、利用待定系数法求直线的解析式、等腰三角形的判定和性质、勾股定理、旋转的性质、动点运动问题以及最短路径问题,第三问有难度,采取了分类讨论的思想,并与方程相结合,利用勾股定理和等腰三角形的性质列方程解决问题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 时间段 | 频数 | 频率 |
| 29分钟及以下 | 108 | 0.54 |
| 30-39分钟 | 24 | 0.12 |
| 40-49分钟 | m | 0.15 |
| 50-59分钟 | 18 | 0.09 |
| 1小时及以上 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
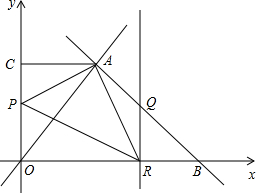 如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.
如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,且使A′B′经过点A.
如图,△ABC是直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,且使A′B′经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
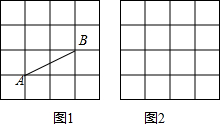 如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.
如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com