
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() .
.
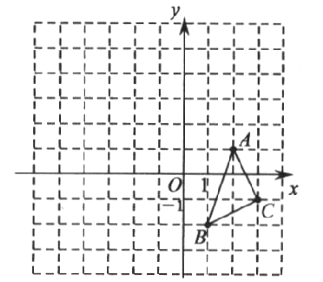
(1)画出![]() ,使
,使![]() 与
与![]() 关于点
关于点![]() 成中心对称,并写出点
成中心对称,并写出点![]() 的对应点
的对应点![]() 的坐标_____________;
的坐标_____________;
(2)以原点![]() 为位似中心,位似比为1:2,在
为位似中心,位似比为1:2,在![]() 轴的左侧,画出将
轴的左侧,画出将![]() 放大后的
放大后的![]() ,并写出点
,并写出点![]() 的对应点
的对应点![]() 的坐标___________________;
的坐标___________________;
(3)![]() ___________________.
___________________.
【答案】(1)画图见解析,![]() ;(2)画图见解析,
;(2)画图见解析,![]() ;(3)
;(3)![]() .
.
【解析】
(1)先作出A、B、C三点关于原点对称的点A1、B1、C1,再顺次连接即可;利用关于原点对称的点的坐标特点即可得出点A1的坐标;
(2)利用位似图形的性质分别作出A、B、C三点的对应点A2、B2、C2,再顺次连接即可;利用位似图形的性质即可得出点A2的坐标;
(3)先根据勾股定理的逆定理判断△ABC的形状,进一步即可求出![]() 的度数,再根据位似图形的性质和特殊角的三角函数值解答即可.
的度数,再根据位似图形的性质和特殊角的三角函数值解答即可.
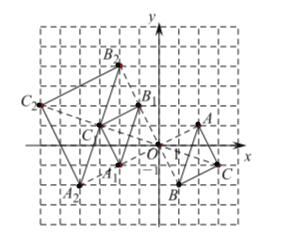
解:(1)如图,![]() 即为所求,
即为所求,![]() ,故答案为:
,故答案为:![]() ;
;
(2)如图![]() 即为所求,
即为所求,![]() ,故答案为:
,故答案为:![]() ;
;
(3)∵![]() ,∴
,∴![]() ,∴∠ACB=90°,AC=BC,∴∠BAC=45°,
,∴∠ACB=90°,AC=BC,∴∠BAC=45°,
∴![]() .
.
故答案为:![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进30海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.
x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.
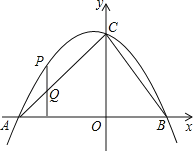
(1)求A,C两点的坐标.
(2)请用含a的代数式表示线段PQ的长,并求出a为何值时PQ取得最大值.
(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以B,C,Q为顶点的三角形是等腰三角形?若存在,请写出此时点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .抛物线上有一点
.抛物线上有一点![]() ,且
,且![]() .
.
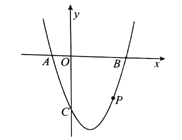
(1)求抛物线的解析式和顶点坐标.
(2)当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值.
面积的最大值.
(3)①设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .求
.求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,点
时,点![]() 的坐标是___________.
的坐标是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
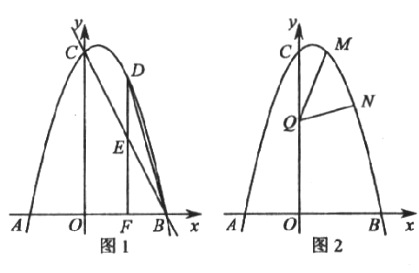
(1)求此抛物线的表达式及顶点的坐标;
(2)若点![]() 是
是![]() 轴上方抛物线上的一个动点(与点
轴上方抛物线上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连结
,连结![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
①试用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
②直线![]() 能否把
能否把![]() 分成面积之比为1:2的两部分?若能,请求出点
分成面积之比为1:2的两部分?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
(3)如图2,若点![]() 也在此抛物线上,问在
也在此抛物线上,问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,请直接写出点
?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数![]() 的图象经过点C,一次函数
的图象经过点C,一次函数![]() 的图象经过点C,一次函数
的图象经过点C,一次函数![]() 的图象经过点A.
的图象经过点A.
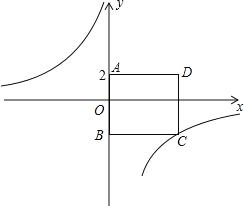
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com