
【题目】反比例函数![]() 在第一象限上有两点A,B.
在第一象限上有两点A,B.
(1)如图1,AM⊥y轴于M,BN⊥x轴于N,求证:△AMO的面积与△BNO面积相等;
(2)如图2,若点A(2,m),B(n,2)且△AOB的面积为16,求k值.
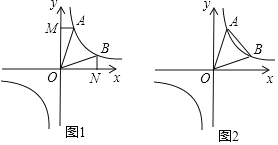
【答案】(1)见解析;(2)12.
【解析】
(1)根据反比例函数的k值的含义即可证明,
(2)过点A作AC⊥x轴,则AM=2,AC=m,BN=2,CN=n-2,根据S△AOB=S四边形ACOM+S梯形ACBN-S△AOM-S△BON,列出其面积的表示式子又m=n,即可化简得![]() ,得m=6,故求出k值
,得m=6,故求出k值
(1)设某点A(x1,y1),B(x2,y2)
∵A,B都在反比例函数![]() 上,
上,
∴x1y1=x2y2,
∴S△AMO=![]() x1y1=S△BNO=
x1y1=S△BNO=![]() x2y2
x2y2
即△AMO的面积与△BNO面积相等;
(2)过点A作AC⊥x轴,
则AM=2,AC=m,BN=2,CN=n-2,
S△AOB=S四边形ACOM+S梯形ACBN-S△AOM-S△BON,
即16=2m+![]() (2+m)(n-2)-
(2+m)(n-2)-![]() ×2×2m
×2×2m
∵m=n
∴可化简为![]() ,
,
∴m=6,(-6舍去)
∴k=2m=12.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
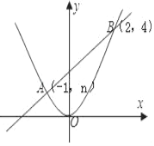
【题目】如图,一次函数y1=kx+b与二次函数y2=ax2的图象交于A(﹣1,n),B(2,4)两点.
(1)利用图中条件,求两个函数的解析式;
(2)根据图象直接写出使y1<y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本学期初三期中调研测试数学试题的命题质量与难度系数,命题教师选取了一个水平相当的初三年级进行分析研究,随机抽取部分学生成绩(得分为整数,满分为130分)分为5组:第一组55~70,第二组70~85,第三组85~100,第四组100~115,第五组115~130;统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
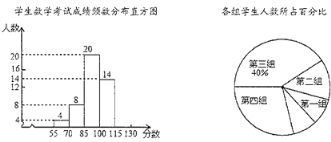
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于70分评为“D”,70~100分评为“C”,100~115分评为“B”,115~130分评为“A”,那么该年级1500名考生中,考试成绩评为“B”的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的一部分如图所示,给出以下结论:
图象的一部分如图所示,给出以下结论:![]() ;
;![]() 当
当![]() 时,函数有最大值;
时,函数有最大值;![]() 方程
方程![]() 的解是
的解是![]() ,
,![]() ;
;![]() ,其中结论错误的个数是
,其中结论错误的个数是![]()
![]()
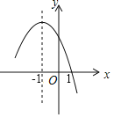
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD内接于![]() ,对角线AC和BD相交于点E,AC是
,对角线AC和BD相交于点E,AC是![]() 的直径.
的直径.
![]() 如图1,连接OB和OD,求证:
如图1,连接OB和OD,求证:![]() ;
;
![]() 如图2,延长BA到点F,使
如图2,延长BA到点F,使![]() ,在AD上取一点G,使
,在AD上取一点G,使![]() ,连接FG和FC,过点G作
,连接FG和FC,过点G作![]() ,垂足为M,过点D作
,垂足为M,过点D作![]() ,垂足为N,求
,垂足为N,求![]() 的值;
的值;
![]() 如图3,在
如图3,在![]() 的条件下,点H为FG的中点,连接DH交
的条件下,点H为FG的中点,连接DH交![]() 于点K,连接AK,若
于点K,连接AK,若![]() ,
,![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以等边三角形 ABC 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形就是“勒洛三角形”(勒洛 三角形是定宽曲线所能构成的面积最小的图形),若 AB=2,则勒洛三角形的面积为( )
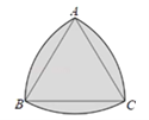
A. π+ ![]() B. π-
B. π-![]() C. 2π+2
C. 2π+2 ![]() D. 2π-2
D. 2π-2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某楼盘准备以每平方米15000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米12150元的均价开盘销售
![]() 求平均每次下调的百分率.
求平均每次下调的百分率.
![]() 某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
![]() 打
打![]() 折销售;
折销售;![]() 不打折,一次性送装修费每平方米250元.
不打折,一次性送装修费每平方米250元.
试问哪种方案更优惠?比另外一种方案优惠多少元?![]() 不考虑其他因素
不考虑其他因素![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)B点坐标为 ,并求抛物线的解析式;
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,直接写出此时点P的坐标.
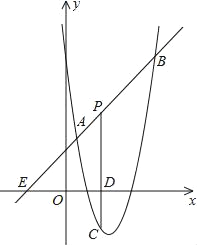
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com