
����Ŀ��̽���뷢�֣�
��ͼ1��ʾ��ͼ�Σ������dz�����ѧϰ��Ʒ����Բ�森���Dz���������ͼ�ν���������ͼ������ô����һ����ͼ���У�������������Щ��ѧ֪ʶ�أ���������㷢����Ĵ������ǣ�����������⣺
��1���۲�������ͼ������̽����BDC���A����B����C֮��Ĺ�ϵ����˵�����ɣ�
��2������ֱ���������Ͻ��ۣ���������������⣺
����ͼ2����һ�����dz�XYZ��������ABC�ϣ�ʹ���dzߵ�����ֱ�DZ�XY��XZǡ�þ�����B��C������A=50�������ABX+��ACX=__________�㣻
����ͼ3��DCƽ�֡�ADB��ECƽ�֡�AEB������DAE=50�㣬��DBE=130�������DCE�Ķ�����
����ͼ4����ABD����ACD��10�ȷ����ཻ�ڵ�G1��G2����G9������BDC=140�㣬��BG1C=77�������A�Ķ�����

���𰸡���1����BDC=��A+��B+��C����2����40�㣻�ڡ�DCE=90�㣻�ۡ�A =70�㣮
�����������������(1)������AD���ӳ�����F��������ǵ����ʵó���BDF=��BAD+��B����CDF=��C+��CAD���Ӷ��ó���������Ҫ�Ľ��ۣ�(2)���������ݵ�һ��Ľ��۵ó��𰸣��������ݵ�һ��Ľ��۵ó���ADB+��AEB=80����Ȼ�������DCE=![]() ����ADB+��AEB��+��A�ó��𰸣�������������ó���BG1C=
����ADB+��AEB��+��A�ó��𰸣�������������ó���BG1C=![]() ����ABD+��ACD��+��A��Ȼ������AΪx����������ABD+��ACD=140��-x���ó���.
����ABD+��ACD��+��A��Ȼ������AΪx����������ABD+��ACD=140��-x���ó���.
���������(1)������AD���ӳ�����F������Ƕ����ɵ���BDF=��BAD+��B����CDF=��C+��CAD��
����BDC=��BDF+��CDF����BAC=��BAD+��CAD����ӿɵ���BDC=��A+��B+��C��
(2)�������ɣ�1���Ľ����ã���ABX+��ACX+��A=��BXC�� ����Ϊ��A=50������BXC=90����
������ABX+��ACX=90��-50��=40����
�����ɣ�1���Ľ�������DBE=��A+��ADB+��AEB������ADB+��AEB=80����
����DCE=![]() ����ADB+��AEB��+��A�� ������DAE=50������DBE=130��������DCE=90����
����ADB+��AEB��+��A�� ������DAE=50������DBE=130��������DCE=90����
������BG1C=![]() ����ABD+��ACD��+��A�� �ߡ�BG1C=77���� ������AΪx����
����ABD+��ACD��+��A�� �ߡ�BG1C=77���� ������AΪx����
�ߡ�ABD+��ACD=140��-x�� ��![]() ��140-x��+x=77��x=70 ���AΪ70����
��140-x��+x=77��x=70 ���AΪ70����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ���AD��E����BA���ӳ����ڵ�F��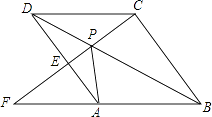
��1����֤����APD�ա�CPD��
��2����֤����APE�ס�FPA��
��3�����룺�߶�PC��PE��PF֮�����ʲô��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У�����֤����ABD�ա�ACD���ǣ� ����

A. BD=DC��AB=AC B. ��ADB=��ADC��BD=DC
C. ��B=��C����BAD=��CAD D. ��B=��C��BD=DC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������²������ڵ���������ABC�У�AB= AC��ADƽ����BAC����BC�ڵ�D.����ABD������ֱ��AD����ԳƱ任�����õ�������ACD�غ�.
�������н���:����ͬһ���������У��ȽǶԵȱ�;����ͬһ���������У��ȱ߶ԵȽ�;
�����������εĶ���ƽ���ߡ��ױ��ϵ����ߺ����غ�.
�����������ɵó����� �� (����ȷ���۵���Ŷ�����).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����ABC��������AD��BE�ཻ�ڵ�H����AD=BD����˵�����н��۳��������ɡ���1����DBH=��DAC����2����BDH�ա�ADC.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��ȡ��D���E��ʹ��AD=AE����BAE=��CAD������BD��CE���ڵ�O����֤��

��1����ABD�ա�ACE��
��2��OB=OC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������Ϊ��E������DE��FΪ�߶�DE��һ�㣬�ҡ�AFE=��B��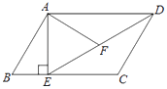
��1����֤����ADF�ס�DEC��
��2����AB=4��AD=3![]() �� AF=2
�� AF=2![]() �� ��AE�ij���
�� ��AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��BE��AC��E����D��E�ֱ���AB��AC���е㣮�ӳ�BC����F��ʹCF=CE��

��1������ABC�Ķ�����
��2����֤��BE=FE��
��3����AB=2������CEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
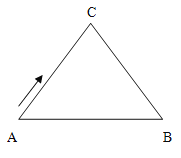
����Ŀ����ͼ����ABC����AC��BC��10 cm��AB��12 cm����D��AB���е�������CD������P�ӵ�A��������A��C��B��·���˶��������Bʱ�˶�ֹͣ���ٶ�Ϊÿ��2 cm�����˶�ʱ��Ϊ![]() ����
����
��1����CD�ij���
��2����![]() Ϊ��ֵʱ����ADP��ֱ����������
Ϊ��ֵʱ����ADP��ֱ����������
��3��ֱ��д������![]() Ϊ��ֵʱ����ADP�ǵ�����������
Ϊ��ֵʱ����ADP�ǵ�����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com