
 如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.
如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3. 分析 过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=45°,进而可得出答案.
解答  解:过点B作BM⊥FD于点M,
解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=2$\sqrt{3}$,
∴∠ABC=30°,BC=AC×tan60°=2$\sqrt{3}$×$\sqrt{3}$=6.
∵AB∥CF,
∴BM=BC×sin30°=6×$\frac{1}{2}$=3,
CM=BC×cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=3,
∴CD=CM-MD=3$\sqrt{3}$-3.
故答案为:3$\sqrt{3}$-3.
点评 本题考查的是勾股定理、直角三角形的性质及平行线的性质,难度较大,解答此类题目的关键根据题意建立三角形利用所学的三角函数的关系进行解答.


科目:初中数学 来源: 题型:填空题
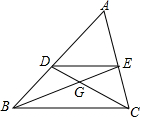 如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形按边分可分为不等边三角形、等腰三角形 | |
| B. | 等腰三角形的内角可能是钝角或直角 | |
| C. | 三角形外角一定是钝角 | |
| D. | 三角形的中线把三角形分成面积相等的两部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
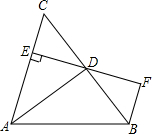 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
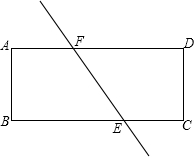 如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.
如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com