
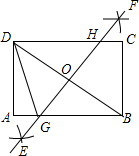
 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )| A. | $\frac{25}{8}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{8}$ |
分析 由矩形的性质得出AD=BC=3,∠A=90°,由线段垂直平分线的性质得出DG=BG,设AG=x,则DG=BG=4-x,由勾股定理得出方程,解方程即可.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=3,∠A=90°,
∵EF是BD的垂直平分线,
∴DG=BG,
设AG=x,则DG=BG=4-x,
在Rt△ADG中,由勾股定理得:AD2+AG2=DG2,
即32+x2=(4-x)2,
解得:x=$\frac{7}{8}$;
即AG的长为$\frac{7}{8}$;
故选:C.
点评 本题考查了矩形的性质、线段垂直平分线的性质、勾股定理;熟练掌握矩形的性质,由勾股定理得出方程是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
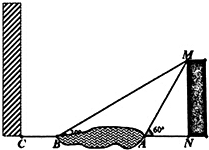 根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.
根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=-11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-7}\\{y=5}\\{z=-11}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=11}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
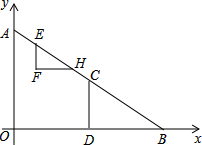 已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).
已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com