练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．一只不透明的袋子中装有一些红球和白球，这些球除颜色外都相同．将球摇匀，从中任意摸出一个球，摸到红球是（　　）
    A．确定事件B．必然事件C．不可能事件D．随机事件

    分析 根据事件发生的可能性大小判断相应事件的类型即可．

    解答 解：一只不透明的袋子中装有一些红球和白球，这些球除颜色外都相同．将球摇匀，从中任意摸出一个球，摸到红球是随机事件，
    故选：D．

    点评 本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．将不等式$\left\{\begin{array}{l}{2x+16＜8x-2}\\{\frac{1}{2}x≤8-\frac{3}{2}x}\end{array}\right.$的解集在数轴上表示出来，正确的是（　　）
    A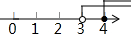．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知过一个多边形的一个顶点的所有对角线共有5条，则这个多边形的内角和为（　　）
    A．720°B．1080°C．1260°D．1440°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

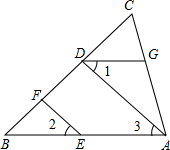    11．请完成下面的证明过程：
    如图，EF∥AD，∠1=∠2，
    求证：∠BAC+∠DGA=180°．
    证明：∵EF∥AD（已知）
    ∴∠2=∠3（两直线平行，同位角相等）
    ∵∠1=∠2（已知）
    ∴∠1=∠3（等量代换）
    ∴AB∥DG（内错角相等，两直线平行）
    ∴∠BAC+∠DGA=180°（两直线平行，同旁内角互补）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算：
    （1）（2-3$\sqrt{3}$）（2+3$\sqrt{3}$）-（3$\sqrt{3}$-2）2
    （2）$\sqrt{18}$-$\frac{\sqrt{32}-\sqrt{8}}{\sqrt{2}}$+（-$\sqrt{12}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先化简$（\frac{1}{a+1}+\frac{{{a^2}-2a+1}}{{{a^2}-1}}）÷\frac{a-1}{a+1}$，再选择一个恰当的a的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解不等式（组）：
    （1）$\frac{x+6}{2}＜1-\frac{2x+1}{3}$；        
    （2）$\left\{\begin{array}{l}3（x-1）＜5x+1\\ 2x-4≤\frac{x-1}{2}\end{array}\right.$，并写出其整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

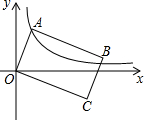    11．如图，已知点A是反比例函数y=$\frac{{\sqrt{6}}}{x}$在第一象限图象上的一个动点，连接OA，以$\sqrt{3}$OA为长，OA为宽作矩形AOCB，且点C在第四象限，随着点A的运动，点C也随之运动，但点C始终在反比例函数y=$\frac{k}{x}$的图象上，则k的值为（　　）
    A．-3$\sqrt{6}$B．3$\sqrt{6}$C．-$\sqrt{6}$D．3$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．2022年将在北京---张家口举办冬季奥运会，很多学校开设了相关的课程．某校8名同学参加了滑雪选修课，他们被分成甲、乙两组进行训练，身高（单位：cm）如下表所示：
    队员1队员2队员3队员4
    甲组176177175176
    乙组178175177174
    设两队队员身高的平均数依次为${\overline x_甲}$，${\overline x_乙}$，方差依次为$S_甲^2$，$S_乙^2$，则下列关系中完全正确的是（　　）
    A．$\overline{x_甲}＞\overline{x_乙}，S_甲^2＞S_乙^2$B．$\overline{x_甲}=\overline{x_乙}，S_甲^2＞S_乙^2$
    C．$\overline{x_甲}＜\overline{x_乙}，S_甲^2＜S_乙^2$D．$\overline{x_甲}=\overline{x_乙}，S_甲^2＜S_乙^2$

    查看答案和解析>>

    同步练习册答案