解:(1)∵抛物线y=ax
2-2ax+b过A(3,0),B(0,-

),
∴0=9a-6a+b-

=b,
解得a=

,b=-

,
∴抛物线解析式为y=
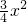
-
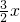
-

.
(2)(x
p,y
p),△PDA的面积为S
1,△POB的面积为S
2,
∵A(3,0),B(0,-

),
∴OA=3,OB=

,
∴S
1=

OA•|y
p|=

|y
p|,S
2=

OB•|x
p|=

|x
p|,3分
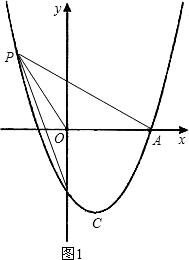
∵P点在第二象限,
∴S
1=

y
p,S
2=-

x
p,
∵S
1=2s
2∴y
p=-

x
p,
∵点P在抛物线上,
∴y
p=

x
p2-

x
p-

,
-

x
p=

x
p2-

x
p-

,
解得,x
p=

(舍去),x
p=-

,
当x
p=-

时,y
P=
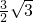
,
∴点P的坐标为(-

,

).
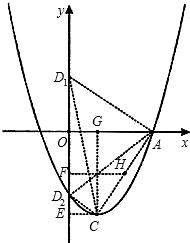
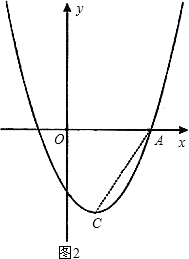
(3)∵C为抛物线的顶点,
∴C点的坐标为(1,-3),过点C作CE⊥y轴于点E,CG⊥x轴于点G,则CE=1,CG=3,
要使△ADC为直角三角形,分三种情况讨论:
①以AC为斜边,则D在以AC为直径的圆上,取AC的中点H,OE的中点F,连接HF,则HF为直角梯形OECA的中位线,HF=

(EC+OA)=2,即圆心H到y轴的距离为2,
在Rt△CGA中,
∵CG=3,AG=2,
∴AC=

,AH=

,
∵

<2,
∴y轴与⊙H相离,
∴y轴上不存在符合条件的D点.
②以CD为斜边,过点A作AD
1⊥AC交y轴于点D
1,
∵∠D
1AO+∠OAC=90°,∠GCA+∠GAC=90°,
∴∠D
1AO=∠ACG,
∵AO=CG,
∴Rt△D
1A0≌Rt△ACG,
∴D
1O=AG=2,
∴y轴上存在点D
1(0,2)使△D
1AC为直角三角形.
③以AD为斜边,过点C作CD
2⊥AC交y轴于点D
2,
∵∠D
2CA=90°,∠GCE=90°,
∴∠D
2GE=∠ACG,
∴Rt△ACG∽Rt△D
2CE,
∴
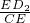
=
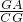
=

,
∵CE=1,
∴ED
2=

,
∵OE=3,
∴OD
2=OE-ED
2=

,
∴y轴上存在点D
2(0,-

)使△D
2AC为直角三角形.
分析:(1)把已知坐标代入抛物线求出a,b的值后易求抛物线的解析式.
(2)求出OA,OB的值后可求出S
1,S
2.根据题意求出点P的坐标.
(3)易求出C点的坐标,过点C作CE⊥y轴于点E,CG⊥x轴于点G,要使△ADC为直角三角形,可分三种情况讨论(以AC为斜边,则D在以AC为直径的圆上,取AC的中点H,OE的中点F,连接HF;以CD为斜边,过点A作AD
1⊥AC交y轴于点D
1;以AD为斜边,过点C作CD
2⊥AC交y轴于点D
2),利用相似三角形的判定以及线段比求解.
点评:本题考查的是二次函数的有关知识以及相似三角形的判定等知识.考生要注意的是全面分析问题,分情况解答.

 )
)
 ),
), =b,
=b, ,b=-
,b=- ,
,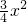 -
-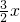 -
- .
. ),
), ,
, OA•|yp|=
OA•|yp|= |yp|,S2=
|yp|,S2= OB•|xp|=
OB•|xp|= |xp|,3分
|xp|,3分 yp,S2=-
yp,S2=- xp,
xp, xp,
xp, xp2-
xp2- xp-
xp- ,
, xp=
xp= xp2-
xp2- xp-
xp- ,
, (舍去),xp=-
(舍去),xp=- ,
, 时,yP=
时,yP=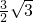 ,
, ,
, ).
). (EC+OA)=2,即圆心H到y轴的距离为2,
(EC+OA)=2,即圆心H到y轴的距离为2, ,AH=
,AH= ,
, <2,
<2,
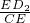 =
=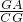 =
= ,
, ,
, ,
, )使△D2AC为直角三角形.
)使△D2AC为直角三角形.

 教学练新同步练习系列答案
教学练新同步练习系列答案 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=