【题目】先化简，再计算： (b＋2a) (b－2a)－(b－3a)2，其中a＝－1，b＝－2．
科目：初中数学 来源： 题型：
【题目】问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是：将ΔBCD绕点D逆时针旋转90°到ΔAED处，点B、C分别落在点A、E处（如图②），易证点C、A、E在同一条直线上，并且ΔCDE是等腰直角三角形，所以CE＝
CD，从而得出结论：AC+BC＝
CD.
图① 图② 图③ 图④
简单应用：
（1）在图①中，若AC＝
，BC＝2
，则CD＝ .
（2）如图③，AB是⊙O的直径，点C、D在⊙O上，弧AD＝弧BD，若AB＝13，BC＝12，求CD的长.
拓展延伸：
（3）如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m<n），求CD的长（用含m，n的代数式表示）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列各式从左到右的变形中，是因式分解的为（ ）
A. ab+ac+d＝a（b+c）+dB. （x+2）（x﹣2）＝x2﹣4
C. 6ab＝2a3bD. x2﹣8x+16＝（x﹣4）2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长为3，E，F 分别是AB，BC边上的点，且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.
（1）求证：EF=FM；
（2）当AE=1时，求EF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．
（1）求证：AB是⊙O的切线．
（2）已知AO交⊙O于点E，延长AO交⊙O于点D，tanD=
，求
的值．
（3）（3分）在（2）的条件下，设⊙O的半径为3，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
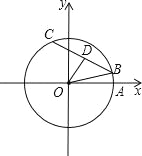
【题目】如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与⊙O交于B、C两点，则弦BC的长的最小值为（ ）.
A．22 B．24 C．10
D．12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于函数y=3x﹣1，下列说法正确的是（ ）
A. 它的图象过点（3，﹣1） B. y值随着x值增大而减小
C. 它的图象经过第二象限 D. 当x＞1时，y＞0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，若点M是x轴正半轴上的任意一点，过点M作PQ∥y轴，分别交函数
（x＞0）和
（x＞0）的图象于点P和Q，连接OP、OQ,则下列结论正确的是（ ）
A. ∠POQ不可能等于900 B. 
C. 这两个函数的图象一定关于x轴对称 D. △POQ的面积是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
