
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表
学生借阅图书的次数
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
学生借阅图书的次数统计表

请你根据统计图表的信息,解答下列问题:
(1)a= ;b=
(2)该调查统计数据的中位数是__________次
(3)扇形统计图中,“3次”所对应的扇形圆心角度数是______________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次以上”的人数
【答案】(1)17,20;(2)2;(3)72°;(4)120
【解析】
(1)先由1次的人数及其所占百分比求得总人数,总人数减去其他次数的人数求得a的值,用3次的人数除以总人数求得b的值;
(2)根据中位数和众数的定义求解;
(3)用360°乘以“3次”对应的百分比即可得;
(4)用总人数乘以样本中“4次及以上”的人数所占比例即可得.
解:(1)∵被调查的总人数为13÷26%=50人,
∴a=50-(7+13+10+3)=17,b%=![]() ×100%=20%,即b=20,
×100%=20%,即b=20,
故答案为:17、20;
解析:被调查的总人数![]()
![]() ;
;
(2)由于共有50人,其中位数是第25,26个数据的平均数,而第25,26个数据均为2次,所以中位数是2次;
故答案为:2;
(3)扇形统计图中“3次”所对应的圆心角度数为![]() ,
,
故答案为:72°;
(4)估计该校学生一周内借阅图书“4次以上”的人数![]() 人.
人.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 点
点![]() .
.
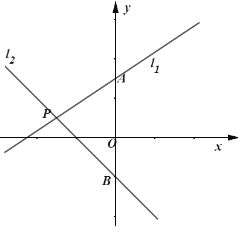
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)过动点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,且
两点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②若![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
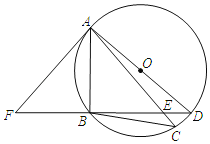
【题目】如图,AD是⊙O的直径,弧BA=弧BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
(1)求证:AF是⊙O的切线;
(2)求证:△ABE∽△DBA;
(3)若BD=8,BE=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
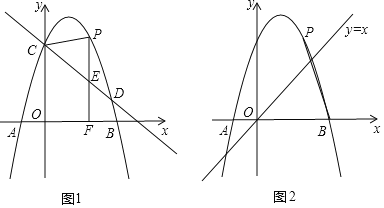
【题目】如图1所示,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上的一个动点,过
是抛物线上的一个动点,过![]() 点作
点作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]()
(1)求抛物线的解析式
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的坐标
的坐标
(3)如图2所示,若点![]() 为对称轴右侧抛物线上一点,连接
为对称轴右侧抛物线上一点,连接![]() ,以
,以![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为
为较长直角边,构造两直角边比为![]() 的
的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 的切线,
的切线,![]() 为弦,连接
为弦,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在一次活动中,对一个数学问题作如下探究:
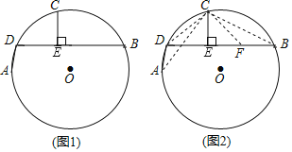
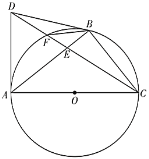
(问题发现)如图1,AD,BD为⊙O的两条弦(AD<BD),点C为![]() 的中点,过C作CE⊥BD,垂足为E.求证:BE=DE+AD.
的中点,过C作CE⊥BD,垂足为E.求证:BE=DE+AD.
(问题探究)小明同学的思路是:如图2,在BE上截取BF=AD,连接CA,CB,CD,CF.……请你按照小明的思路完成上述问题的证明过程.
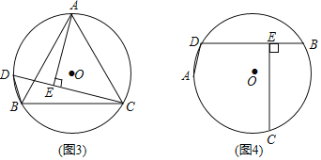
(结论运用)如图3,△ABC是⊙O的内接等边三角形,点D是![]() 上一点,∠ACD=45°,连接BD,CD,过点A作AE⊥CD,垂足为E.若AB=
上一点,∠ACD=45°,连接BD,CD,过点A作AE⊥CD,垂足为E.若AB=![]() ,则△BCD的周长为 .
,则△BCD的周长为 .
(变式探究)如图4,若将(问题发现)中“点C为![]() 的中点”改为“点C为优弧
的中点”改为“点C为优弧![]() 的中点”,其他条件不变,上述结论“BE=DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE、AD、DE之间的新等量关系,并加以证明.
的中点”,其他条件不变,上述结论“BE=DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE、AD、DE之间的新等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() ),连接
),连接![]() 、
、![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 、
、![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,探究线段
顺时针旋转,探究线段![]() 与
与![]() 的数量关系.
的数量关系.
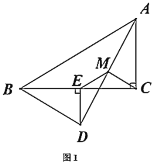
(1)如图1,点![]() 落在
落在![]() 边上时,探究
边上时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
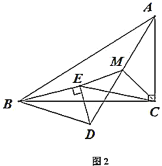
(2)如图2,点![]() 落在
落在![]() 内部时,探究
内部时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com