
【题目】已知关于x的方程x2+3x+ ![]() =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为符合条件的最大整数,求此时方程的根.
【答案】
(1)解:∵关于x的方程x2+3x+ ![]() =0有两个不相等的实数根,
=0有两个不相等的实数根,
∴△=32﹣4×1× ![]() =9﹣3m>0,
=9﹣3m>0,
∴m<3;
(2)解:∵m<3,
∴符合条件的最大整数是2,
∴原方程为x2+3x+ ![]() =0,
=0,
解得:x1= ![]() ,x2=
,x2= ![]()
【解析】根据方程有两个不相等的实数根,可知△>0,由△>0可得到关于m的不等式,求出m的取值范围即可;(2)由(1)中求出的m的取值范围得出符合条件的m的最大整数值,代入原方程,解方程求出方程的根即可.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
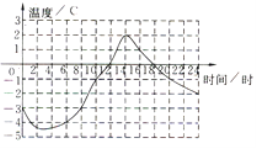
【题目】如图所示的图象记录了某地一月份某天的温度随时间变化.的情况,请你仔细观察图象回答下面的问题:
(1)20时的温度是 ℃,温度是0℃时的时刻是 时,最暖和的时刻是 时,温度在-3℃以下的持续时间为 时;
(2)从图象中还能获取哪些信息?(写出1~2条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
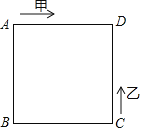
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点,A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2019次相遇在______边上(填AB,BC,CD或AD).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
①请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;
②请画出△ABC绕点B逆时针旋转90°后的△A2BC2 , 并写出点A2、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展.2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的 ![]() 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图一,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上,
①求证:∠BCE+∠BAC=180°;
②当四边形ADCE的周长取最小值时,求BD的长.
(2)若∠BAC![]() 60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)

若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com