
| A. | sin45°=$\frac{\sqrt{3}}{2}$ | B. | tan45°=1 | C. | cos30°=$\frac{1}{2}$ | D. | tan30°=$\frac{\sqrt{3}}{2}$ |
科目:初中数学 来源: 题型:解答题
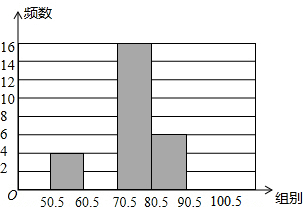 青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.
青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 14 | 0.28 |
| 70.5~80.5 | 16 | a |
| 80.5~90.5 | b | c |
| 90.5~100.5 | 10 | 0.2 |
| 合计 | d | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
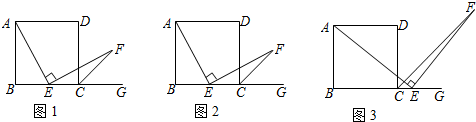
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一定有一个内角为45° | B. | 一定有一个内角为60° | ||
| C. | 一定是直角三角形 | D. | 一定是钝角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
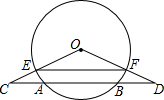 如图,AB是⊙O的弦,C、D是直线AB上的两点,且AC=BD,连接OC、OD,分别交⊙O于E、F两点,试判断EF与CD的位置关系并说明理由.
如图,AB是⊙O的弦,C、D是直线AB上的两点,且AC=BD,连接OC、OD,分别交⊙O于E、F两点,试判断EF与CD的位置关系并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com