
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以PQCD为顶点的四边形是平行四边形是否存在?若存在,直接写出点Q的坐标;若不存在,请说明理由.

【答案】(1)y=﹣x2+4x+5;(2)当m=![]() 时,PE最长;(3)点Q的坐标为(
时,PE最长;(3)点Q的坐标为(![]() ,
,![]() )、(﹣
)、(﹣![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)由点A,B的坐标,利用待定系数法可求出抛物线的解析式;
(2)利用一次函数图象上点的坐标特征可得出点C,D的坐标,进而可得出0<m<4,由点P的横坐标为m可得出点P,E的坐标,进而可得出PE=﹣m2![]() m+2,再利用二次函数的性质即可解决最值问题;
m+2,再利用二次函数的性质即可解决最值问题;
(3)分PE为对角线、PC为对角线、CD为对角线三种情况考虑,由平行四边形的性质(对角线互相平分)结合点P,C,D的坐标可求出点Q的坐标,此题得解.
(1)将A(﹣1,0),B(5,0)代入y=﹣x2+bx+c,得:
![]() ,解得:
,解得:![]() ,∴抛物线的解析式为y=﹣x2+4x+5.
,∴抛物线的解析式为y=﹣x2+4x+5.
(2)∵直线y![]() x+3与y轴交于点C,与x轴交于点D,∴点C的坐标为(0,3),点D的坐标为(4,0),∴0<m<4.
x+3与y轴交于点C,与x轴交于点D,∴点C的坐标为(0,3),点D的坐标为(4,0),∴0<m<4.
∵点P的横坐标为m,∴点P的坐标为(m,﹣m2+4m+5),点E的坐标为(m,![]() m+3),∴PE=﹣m2+4m+5﹣(
m+3),∴PE=﹣m2+4m+5﹣(![]() m+3)=﹣m2
m+3)=﹣m2![]() m+2=﹣(m
m+2=﹣(m![]() )2
)2![]() .
.
∵﹣1<0,0![]() 4,∴当m
4,∴当m![]() 时,PE最长.
时,PE最长.
(3)由(2)可知,点P的坐标为(![]() ).
).
以PQCD为顶点的四边形是平行四边形分三种情况(如图所示):
①以PD为对角线.
∵点P的坐标为(![]() ),点D的坐标为(4,0),点C的坐标为(0,3),∴点Q的坐标为(
),点D的坐标为(4,0),点C的坐标为(0,3),∴点Q的坐标为(![]() 4﹣0,
4﹣0,![]() 0﹣3),即(
0﹣3),即(![]() );
);
②以PC为对角线.
∵点P的坐标为(![]() ),点D的坐标为(4,0),点C的坐标为(0,3),∴点Q的坐标为(
),点D的坐标为(4,0),点C的坐标为(0,3),∴点Q的坐标为(![]() 0﹣4,
0﹣4,![]() 3﹣0),即(
3﹣0),即(![]() );
);
③以CD为对角线.
∵点P的坐标为(![]() ),点D的坐标为(4,0),点C的坐标为(0,3),∴点Q的坐标为(0+4
),点D的坐标为(4,0),点C的坐标为(0,3),∴点Q的坐标为(0+4![]() ,3+0
,3+0![]() ),即(
),即(![]() ).
).
综上所述:在(2)的情况下,存在以PQCD为顶点的四边形是平行四边形,点Q的坐标为(![]() )、(
)、(![]() )或(
)或(![]() ).
).


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】数学课上,小白遇到这样一个问题:
如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() ,求证
,求证![]() ;
;
在此问题的基础上,老师补充:
过点![]() 作
作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,试探究线段
,试探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
小白通过研究发现,![]() 与
与![]() 有某种数量关系;
有某种数量关系;
小明通过研究发现,将三条线段中的两条放到同一条直线上,即“截长补短”,再通过进一步推理,可以得出结论.
阅读上面材料,请回答下面问题:
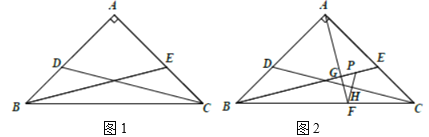
(1)求证![]() ;
;
(2)猜想![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
(3)探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
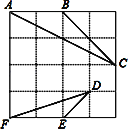
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>kx+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
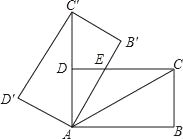
查看答案和解析>>
科目:初中数学 来源: 题型:
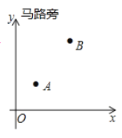
【题目】要在马路边设一个共享单车投放点,向![]() 两家公司提供服务,投放点应设在什么地方,才能使从
两家公司提供服务,投放点应设在什么地方,才能使从![]() 到它的距离之和最短?小明根据实际情况,以马路为
到它的距离之和最短?小明根据实际情况,以马路为![]() 轴建立了如图所示的平面直角坐标系,
轴建立了如图所示的平面直角坐标系,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,则从
,则从![]() 两点到投放点距离之和的最小值是__________,投放点的坐标是__________.
两点到投放点距离之和的最小值是__________,投放点的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座石拱桥的桥拱是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.
为半径的一段圆弧.

![]() 请你确定弧
请你确定弧![]() 的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
![]() 如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为
如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为![]() 米,拱高(即弧的中点到弦的距离)为
米,拱高(即弧的中点到弦的距离)为![]() 米,求桥拱所在圆的半径.
米,求桥拱所在圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com