
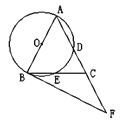
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的 ⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长.
的长.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第二次将点A向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是( )
![]()
A. 12B. 13C. 14D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
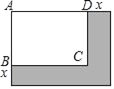
【题目】如图,矩形ABCD的长BC=5,宽AB=3.
(1)若矩形的长与宽同时增加2,则矩形的面积增加 .
(2)若矩形的长与宽同时增加x,此时矩形增加的面积为48,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
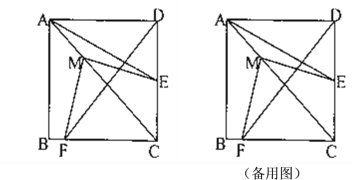
【题目】在正方形![]() 中,点
中,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 是对角线
是对角线![]() 上的动点,连接
上的动点,连接![]() ,过点
,过点![]() 作
作![]() 交正方形的边于点
交正方形的边于点![]() ;
;
(1)当点![]() 在边
在边![]() 上时,①判断
上时,①判断![]() 与
与![]() 的数量关系;
的数量关系;
②当![]() 时,判断点
时,判断点![]() 的位置;
的位置;
(2)若正方形的边长为2,请直接写出点![]() 在
在![]() 边上时,
边上时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
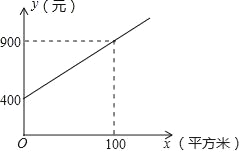
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长线段AB至C使BC=2AB,延长线段BA至D使AD=3AB,点E是线段DB的中点,点F是线段AC的中点,若EF=10cm,求AB、CD的长度

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com