
分析 (1)根据韦达定理可得x1+x2=-4,x1x2=k+1及△=42-4(k+1)≥0,求得k的取值范围,再代入x12x22-x1-x2=29,可得关于k的方程,解方程即可得;
(2)根据(1)中结果可得x1+x2=-4,x1x2=k+1=-3,再带入x12+x22=(x1+x2)2-2x1x2计算即可.
解答 解:(1)∵x1,x2是方程x2+4x+k+1=0的两个实数根,
∴x1+x2=-4,x1x2=k+1,且△=42-4(k+1)≥0,
解得:k≤4,
由x12x22-x1-x2=29可得(k+1)2+4=29,
解得:k1=6(舍),k2=-4;
(2)由(1)知,x1+x2=-4,x1x2=k+1=-3,
∴x12+x22=(x1+x2)2-2x1x2=16+6=22.
点评 本题主要考查一元二次方程根与系数的关系及根的判别式,熟练掌握韦达定理及判别式的值与方程的根的个数是关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 内错角相等 | |
| B. | 同位角互补,两直线平行 | |
| C. | 一个角的余角不等于其自身 | |
| D. | 在同一平面内,过一点能作且只能作一条直线与已知直线垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
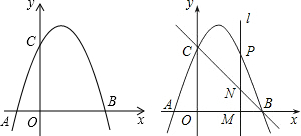
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com