
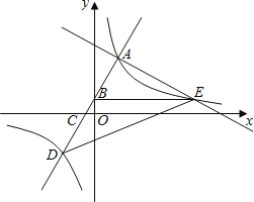
【题目】如图,直线y=2x+b与双曲线y=![]() (k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-
(k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-![]() +n过点A,与双曲线y=
+n过点A,与双曲线y=![]() (k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
(k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
【答案】![]() .
.
【解析】
过点A作AF⊥y轴于点F,过点D作DG⊥y轴于点G,先联立直线AB反比例函数的解析式求出A、D点的横坐标,得到AF与DG,再由三角形的面积比与相似三角形的比例线段得到k与b的关系,进而用b的代数式表示A点坐标,再将其代入AE的解析式中,用b表示n,进而联立AE与反比例函数解析式求出E的坐标,最后根据已知三角形的面积,得到b的方程求得b即可解决问题.
过点A作AF⊥y轴于点F,过点D作DG⊥y轴于点G,
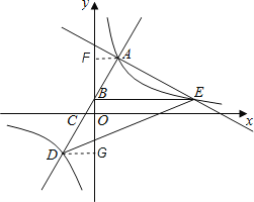
∴AF∥DG,
∴△ABF∽△DBG,
∴![]() ,
,
∵S△ABE:S△DBE=3:4,
∴![]() ,
,
由2x+b=![]() 得,2
得,2![]() +bx-k=0,
+bx-k=0,
解得,x=![]() ,
,
即A点的横坐标为![]() ,D点有横坐标为
,D点有横坐标为![]() ,
,
∴AF=![]() ,DG=
,DG=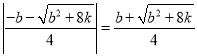 ,
,
∴![]() ,
,
解得,k=6![]() ,
,
∴A点的横坐标为![]() =
=![]() b,纵坐标为
b,纵坐标为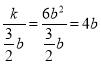 ,
,
∴A(![]() b,4b),
b,4b),
把A(![]() b,4b)代入y=-
b,4b)代入y=-![]() +n中,得n=5b,
+n中,得n=5b,
∴AE的解析式为:y=-![]() +5b,
+5b,
联立方程组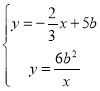 ,
,
解得,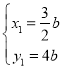 ,
,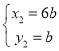 ,
,
∴E(6b,b),
∵B(0,b),
∴BE∥x轴,
∴BE=6b,
∴![]() ,
,
∵S△ABE=4,
∴9![]() =4,
=4,
∴![]() =
=![]() ,
,
∴k=![]() =6×
=6×![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=![]() ,AD=3,点E是边AD靠近A的三等分点,点P是BC延长线上一点,且EP⊥EB,点G是BE上任意一点,过G作GH∥BP,交EP于点H.将△EGH绕点E逆时针旋转α(0<α<90°),得到△EMN(M、N分别是G、H的对应点).
,AD=3,点E是边AD靠近A的三等分点,点P是BC延长线上一点,且EP⊥EB,点G是BE上任意一点,过G作GH∥BP,交EP于点H.将△EGH绕点E逆时针旋转α(0<α<90°),得到△EMN(M、N分别是G、H的对应点).
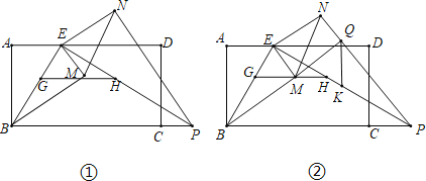
(1)求BP的长;
(2)求![]() 的值;
的值;
(3)如图②当α=60°时,点M恰好落在GH上,延长BM交NP于点Q,取EP的中点K,连接QK.若点G在线段EB上运动,问QK是否有最小值?若有最小值,请求出点G运动到EB的什么位置时,QK有最小值及最小值是多少,若没有最小值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
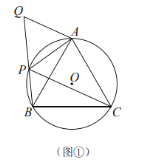
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;
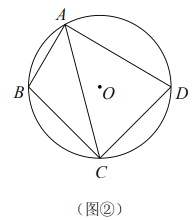
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2![]() ,AB=5.
,AB=5.
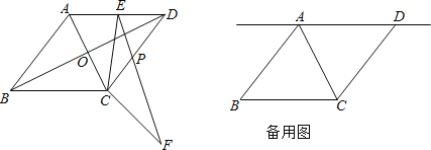
(1)求BD的长;
(2)点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.
①当E为AD的中点时,求EF的长;
②连接AF、DF,当DF的长度最小时,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
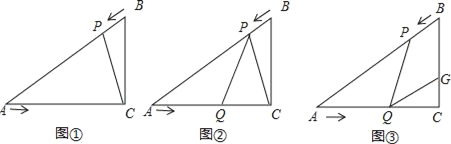
【题目】已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为
cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为![]() cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;
(2)如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;
(3)如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
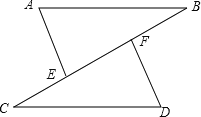
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:BE=CF.
(2)若AB=CF,∠B=40°,求∠D的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com