
【题目】如图,函数![]() 的图象与函数
的图象与函数![]() (x>0)的图象交于A(m,1),B(1,n)两点.
(x>0)的图象交于A(m,1),B(1,n)两点.
(1)求k,m,n的值;
(2)利用图象写出当x≥1时,![]() 和
和![]() 的大小关系.
的大小关系.
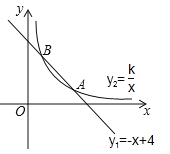
【答案】(1)k=3,m=3,n=3;(2)当1<x<3时,![]() ;当x>3时,
;当x>3时,![]() ;当x=1或x=3时,
;当x=1或x=3时,![]() .
.
【解析】
试题分析:(1)把A与B坐标代入一次函数解析式求出m与a的值,确定出A与B坐标,将A坐标代入反比例解析式求出k的值即可;
(2)根据B的坐标,分x=1或x=3,1<x<3与x>3三种情况判断出![]() 和
和![]() 的大小关系即可.
的大小关系即可.
试题解析:(1)把A(m,1)代入一次函数解析式得:1=﹣m+4,即m=3,∴A(3,1),把A(3,1)代入反比例解析式得:k=3,把B(1,n)代入一次函数解析式得:n=﹣1+4=3;
(2)∵A(3,1),B(1,3),∴由图象得:当1<x<3时,![]() ;当x>3时,
;当x>3时,![]() ;当x=1或x=3时,
;当x=1或x=3时,![]() .
.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】若(x-9)(2x-n)=2x2+mx-18,则m、n的值分别是( )
A. m=-16,n=-2B. m=16,n=-2C. m=-16,n=2D. m=16,n=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月16日记者从我省某市医保局获悉,对于符合减半征收条件的企业2月已缴纳的社会基本医疗保险费实施差额退款,已累计为262000家企业办理退款74315000元.将数74315000用科学记数法表示为 ( )
A.7.4315×108B.0.74315×108C.7.4315×107D.7.4315×106
查看答案和解析>>
科目:初中数学 来源: 题型:
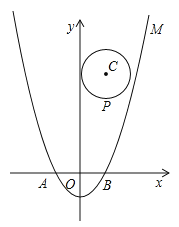
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】命题“如果两个角相等,那么它们都是直角”的逆命题是( )
A.如果两个角不相等,那么它们都不是直角
B.如果两个角都不是直角,那么这两个角不相等
C.如果两个角都是直角,那么这两个角相等
D.相等的两个角都是直角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com