
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?
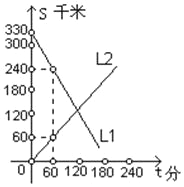
【答案】(1)L1表示汽车B到甲地的距离与行驶时间的关系;(2)1.5千米/分;(3)s2=t;(4)30千米;(5)132分钟.
【解析】试题分析:(1)直接根据函数图象的走向和题意可知L1表示汽车B到甲地的距离与行驶时间的关系;
(2)由L1上60分钟处点的坐标可知路程和时间,从而求得速度;
(3)先分别设出函数,利用函数图象上的已知点,使用待定系数法可求得函数解析式;
(4)结合(3)中函数图象求得![]() 时s的值,做差即可求解;
时s的值,做差即可求解;
(5)求出函数图象的交点坐标即可求解.
试题解析:(1)函数图形可知汽车B是由乙地开往甲地,故L1表示汽车B到甲地的距离与行驶时间的关系;
(2)(330﹣240)÷60=1.5(千米/分);
(3)设L1为![]() 把点(0,330),(60,240)代入得
把点(0,330),(60,240)代入得
![]() 所以
所以![]()
设L2为![]() 把点(60,60)代入得
把点(60,60)代入得
![]()
所以![]()
(4)当![]() 时,
时,![]()
330﹣150﹣120=60(千米);
所以2小时后,两车相距60千米;
(5)当![]() 时,
时,![]()
解得![]()
即行驶132分钟,A、B两车相遇.


科目:初中数学 来源: 题型:
【题目】一自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产记为负
(1)根据记录的数据可知该厂星期四生产自行车多少辆?
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产自行车多少辆?
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超出部分每辆另加15元,少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A(0,4),点B(m,0),以AB为边在右侧作正方形ABCD.
(1)当点B在x轴正半轴上运动时,求点C点的坐标.(用m表示)
(2)当m=0时,如图2,P为OA上一点,过点P作PM⊥PC,PM=PC,连MC交OD于点N,求AM+2DN的值;
(3)如图3,在第(2)问的条件下,E、F分别为CD、CO上的点,作EG∥x轴交AO于G,作FH∥y轴交AD于H,K是EG与FH的交点.若S四边形KFCE=2S四边形AGKH,试确定∠EAF的大小,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车3辆,B型公交车2辆,共需600万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
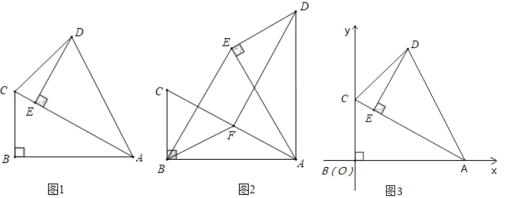
【题目】在![]() 中,∠ABC=90°,∠BAC=30°,将
中,∠ABC=90°,∠BAC=30°,将![]() 绕点A顺时针旋转一定的角度α得到
绕点A顺时针旋转一定的角度α得到![]() ,点B、C的对应点分别是E、D.
,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若α=60°时,点F是边AC中点,求证:DF=BE;
(3)如图3,点B、C的坐标分别是(0,0),(0,2),点Q是线段AC上的一个动点,点M是线段AO上的一个动点,是否存在这样的点Q、M使得![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
为直角三角形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
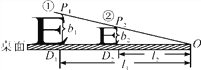
【题目】如图所示,在水平桌面上的两个“E”,当点P1,P2,O在一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力相同.
(1)图中b1,b2,l1,l2满足怎样的关系式?
(2)若b1=3.2 cm,b2=2 cm,①号“E”的测量距离l1=8 cm,要使测得的视力相同,则②号“E”的测量距离l2应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A,B两点,且点A的横坐标为4.点C是双曲线上一点,且纵坐标为8,则△AOC的面积为( )
(k>0)交于A,B两点,且点A的横坐标为4.点C是双曲线上一点,且纵坐标为8,则△AOC的面积为( )
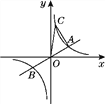
A. 8 B. 32 C. 10 D. 15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com