
已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果
 ,
, ,∠FDE=∠B,那么AF的长为( )
,∠FDE=∠B,那么AF的长为( )
A. B.
B.  C.
C.  D.
D. 
C.
解析试题分析:由AE和CE的长可求出AC的长,因为△ABC是等腰三角形,所以AB=AC,若要求AF 的长,可求出BF的长即可.而通过证明△DBF∽△DCE即可求出BF的长,问题得解.
解:∵AB=AC,
∴∠B=∠C,
∵∠BFD=180°-∠B-∠FDB,∠EDC=180°-∠FDE-∠FDB,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
∴△DBF∽△DCE,
∴BD:CE=BF:CD,
∵BD=2,CD=3,CE=4,
∴2:4=BF:3,
∴BF=1.5,
∵AC=AE+CE= +4=5.5,
+4=5.5,
∴AB=5.5,
∴AF=AB-BF=5.5-1.5=4,
故选C.
考点:1.相似三角形的判定与性质;2.等腰三角形的性质.


科目:初中数学 来源: 题型:解答题
如图,点D、E、F分别在AB、BC、AC上,且DE//AC,EF//AB ,下面写出了证明“∠A+∠B+∠C=180°”的部分过程,请完成填空:
 DE // AC,EF // AB ( )
DE // AC,EF // AB ( )
 ,
,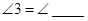 ( )
( ) EF // AB.
EF // AB.
 ( )
( ) DE // AC.
DE // AC.
 ( )
( )
 ( )
( )


 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
对一个图形进行放缩时,下列说法中正确的是( )
| A.图形中线段的长度与角的大小都会改变; |
| B.图形中线段的长度与角的大小都保持不变; |
| C.图形中线段的长度保持不变、角的大小可以改变; |
| D.图形中线段的长度可以改变、角的大小保持不变. |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
| A.3米 | B.4米 | C.4.5米 | D.6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行. 张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
| A.5.5m | B.6.2m | C.11 m | D.2.2 m |
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图,△ABD ≌△EBD, △DBE ≌△DCE, B, E, C在一条直线上.
【小题1】BD是∠ABE的平分线吗?为什么
【小题2】DE⊥BC,BE=EC吗?为什么
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2),(2,3).完成以下问题:
【小题1】请根据题意在图上建立直角坐标系;
【小题2】写出图上其他地点的坐标
【小题3】在图中用点P表示体育馆(-1,-3)的位置
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
下列说法中正确的是( )
①在两个边数相同的多边形中,如果对应边成比例,那么这两个多边形相似;
②如果两个矩形有一组邻边对应成比例,那么这两个矩形相似;
③有一个角对应相等的平行四边形都相似;
④有一个角对应相等的菱形都相似.
| A.①② | B.②③ | C.③④ | D.②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com