
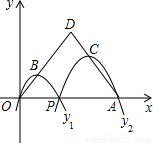

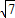 .设P(2x,0),根据二次函数的对称性得出OF=PF=x,推出△OBF∽△ODE,△ACM∽△ADE,得出
.设P(2x,0),根据二次函数的对称性得出OF=PF=x,推出△OBF∽△ODE,△ACM∽△ADE,得出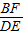 =
=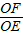 ,
,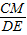 =
=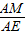 ,代入求出BF和CM,相加即可求出答案.
,代入求出BF和CM,相加即可求出答案.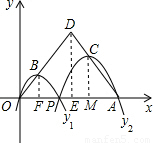 解:过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,
解:过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M, OA=6,
OA=6,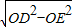 =2
=2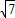 .
.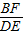 =
=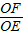 ,
,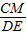 =
=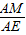 ,
, (OA-OP)=
(OA-OP)= (12-2x)=6-x,
(12-2x)=6-x,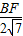 =
=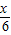 ,
,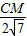 =
=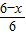 ,
,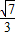 x,CM=2
x,CM=2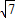 -
-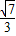 x,
x,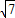 .
.

科目:初中数学 来源: 题型:
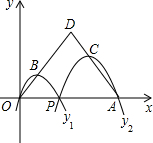 如图,已知点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=8时,这两个二次函数的最大值之和等于( )
如图,已知点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=8时,这两个二次函数的最大值之和等于( )查看答案和解析>>
科目:初中数学 来源: 题型:
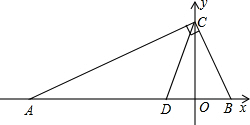 (2012•乌鲁木齐)如图,已知点A(-12,0),B(3,0),点C在y轴的正半轴上,且∠ACB=90°.
(2012•乌鲁木齐)如图,已知点A(-12,0),B(3,0),点C在y轴的正半轴上,且∠ACB=90°.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(-12,0),B(3,0),点C在y轴的正半轴上,且∠ACB=90°.
如图,已知点A(-12,0),B(3,0),点C在y轴的正半轴上,且∠ACB=90°. S△ABC的点P的坐标;
S△ABC的点P的坐标;查看答案和解析>>
科目:初中数学 来源:2012年新疆乌鲁木齐市中考数学试卷(解析版) 题型:解答题
 S△ABC的点P的坐标;
S△ABC的点P的坐标;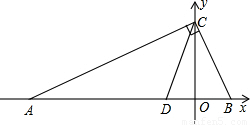
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com