
 如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6m,再前进2米到达点B处时,测得影长MB=1.6m,(图中线段AB、CD、EF表示小明的身高)
如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6m,再前进2米到达点B处时,测得影长MB=1.6m,(图中线段AB、CD、EF表示小明的身高)分析 (1)连接MA、NC并延长,交点即为点O,再连接OE并延长于底面的交点为G,FG即为所求;
(2)过O作OH⊥MG于点H,设DH=xm,根据AB∥CD∥OH得$\frac{MB}{MH}$=$\frac{ND}{NH}$,据此求得DH,再根据$\frac{FG}{HG}$=$\frac{ND}{NH}$可求得FG.
解答 解:(1)如图: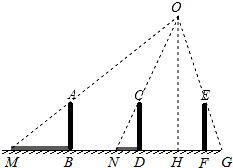
(2)过O作OH⊥MG于点H,设DH=xm,
由AB∥CD∥OH得:$\frac{MB}{MH}$=$\frac{ND}{NH}$,
即$\frac{1.6}{3.6+x}$=$\frac{0.6}{0.6+x}$,
解得x=1.2.
设FG=ym,
同理得$\frac{FG}{HG}$=$\frac{ND}{NH}$,
即$\frac{y}{0.8+y}$=$\frac{0.6}{1.8}$,
解得y=0.4.
所以EF的影长为0.4m.
点评 本题主要考查中心投影,需要把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解即可.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{0008}$=0.2 | B. | $\sqrt{121}=±\sqrt{11}$ | C. | $\root{3}{-\frac{1}{27}}$=-$\frac{1}{3}$ | D. | $\root{3}{-1{0}^{6}}$=-102 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
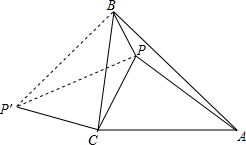 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABD中,∠DAB=90°,AD=1,BD=$\sqrt{17}$,将△ABD沿着CE对折,使得点B与点D重合,折痕为CE.
如图,在Rt△ABD中,∠DAB=90°,AD=1,BD=$\sqrt{17}$,将△ABD沿着CE对折,使得点B与点D重合,折痕为CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com